W pewnym trójkącie równoramiennym największy kąt ma miarę \(120°\), a najdłuższy bok ma długość \(12\) (zobacz rysunek).





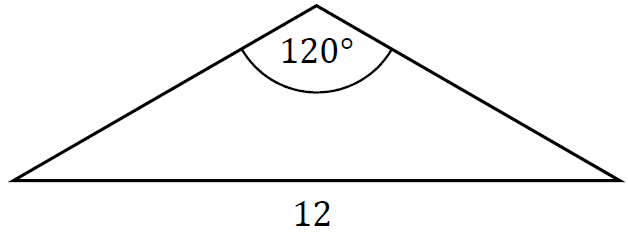
Najkrótsza wysokość tego trójkąta ma długość równą:

A \(6\)
B \(2\sqrt{3}\)
C \(4\sqrt{3}\)
D \(6\sqrt{3}\)

Odpowiedź:      

B

Rozwiązanie:      
Krok 1. Sporządzenie rysunku pomocniczego. Rysując wysokość padającą na bok o znanej nam długości, otrzymamy następującą sytuację: Podzieliliśmy w ten sposób naszą figurę na dwa trójkąty prostokątne o kątach \(30°\), \(60°\) oraz \(90°\) i to z własności tych trójkątów teraz skorzystamy. Krok 2. Obliczenie długości najkrótszej wysokości. Najkrótsza wysokość trójkąta to ta, która pada na najdłuższy bok. W naszym trójkącie najkrótszym bokiem jest podstawa, zatem to wysokość padająca na podstawę będzie tą, której poszukujemy. Z własności trójkątów o kątach \(30°\), \(60°\) oraz \(90\)° wynika, że przyprostokątna leżąca przy kącie o mierze \(30°\) jest \(\sqrt{3}\) razy większa od przyprostokątnej leżącej przy kącie o mierze \(60°\). Mówiąc wprost, jeżeli interesującą nas wysokość opiszemy jako \(x\), to bok o długości \(6\) będzie równy \(x\sqrt{3}\). Skoro tak, to: $$x\sqrt{3}=6 \           ,\ x=\frac{6}{\sqrt{3}} \           ,\ x=\frac{6\cdot\sqrt{3}}{\sqrt{3}\cdot\sqrt{3}} \           ,\ x=\frac{6\sqrt{3}}{3} \           ,\ x=2\sqrt{3}$$

Teoria:      
W trakcie opracowania