Dany jest trójkąt prostokątny \(ABC\) o bokach \(|AC|=24\), \(|BC|=10\), \(|AB|=26\). Dwusieczne kątów tego trójkąta przecinają się w punkcie \(P\) (zobacz rysunek).





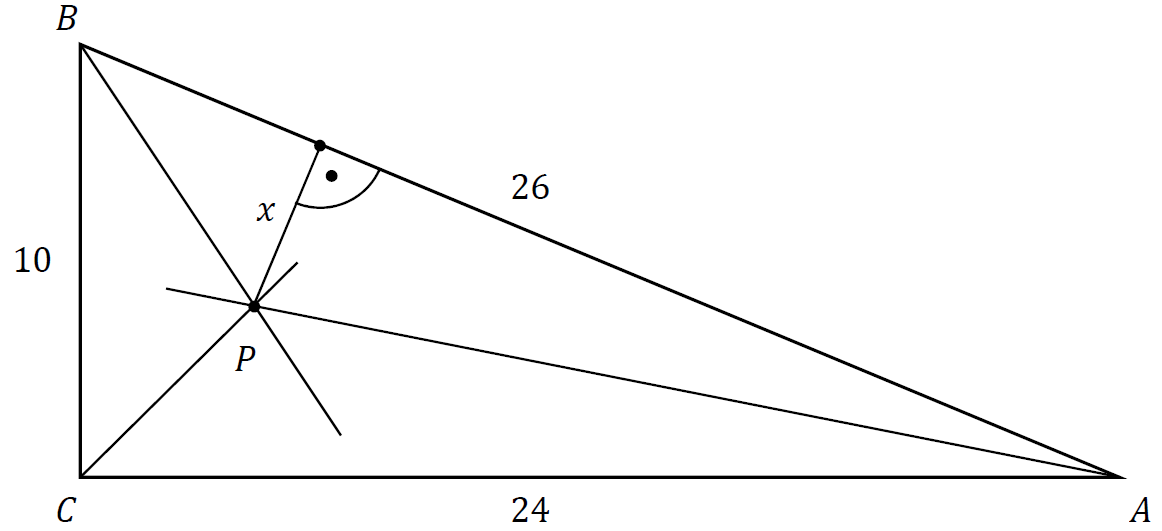
Odległość \(x\) punktu \(P\) od przeciwprostokątnej \(AB\) jest równa:

A \(2\)
B \(4\)
C \(\frac{5}{2}\)
D \(\frac{13}{3}\)

Odpowiedź:      

B

Rozwiązanie:      
Jedną z własności trójkąta prostokątnego jest to, że dwusieczne jego kątów przecinają się w punkcie, który jest jednocześnie środkiem okręgu wpisanego w ten trójkąt. Można więc powiedzieć, że poszukiwana odległość \(x\) to nic innego jak promień okręgu wpisanego w ten trójkąt. Do obliczenia długości takiego promienia możemy skorzystać ze wzoru na promień okręgu wpisanego (który znajduje się w tablicach), czyli: $$r=\frac{a+b-c}{2}$$ Podstawiając teraz do tego wzoru długości boków \(a=24\), \(b=10\) oraz \(c=26\), otrzymamy: $$r=\frac{24+10-26}{2} \           ,\ r=\frac{8}{2} \           ,\ r=4$$

Teoria:      
W trakcie opracowania