Romb ma wymiary podane na rysunku.





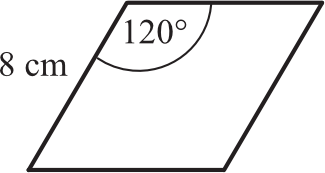
Pole tego rombu jest równe:

A \(72\sqrt{3}cm^2\)
B \(64cm^2\)
C \(32\sqrt{3}cm^2\)
D \(128cm^2\)

Odpowiedź:      

C

Rozwiązanie:      
Krok 1. Obliczenie miary kąta ostrego. Spróbujmy obliczyć miarę kąta ostrego, który znajduje się w tym rombie. Wiemy, że suma kątów przy jednym ramieniu rombu musi być równa \(180°\), zatem kąt ostry ma miarę: $$180°-120°=60°$$ Krok 2. Obliczenie pola rombu. Znając długość boku rombu oraz miarę jego kąta ostrego możemy zastosować "wzór na pole rombu z sinusem", czyli: $$P=a^2\cdot sinα \           ,\ P=8^2\cdot sin60° \           ,\ P=64\cdot\frac{3}{2} \           ,\ P=32\sqrt{3}$$

Teoria:      
W trakcie opracowania