Zbiory arkuszy maturalnych z matematyki. Nasza strona oferuje bogaty wybór przykładowych arkuszy, rozwiązań zadań, testów z matematyki oraz wiele innych materiałów
Matura poprawkowa z matematyki (poziom podstawowy) - Sierpień 2022 Zadanie 19 z 35
Zadanie nr 19. (1pkt)
Punkty \(A\) oraz \(B\) leżą na okręgu o środku \(S\). Kąt środkowy \(ASB\) ma miarę \(100°\). Prosta \(l\) jest styczna do tego okręgu w punkcie \(A\) i tworzy z cięciwą \(AB\) okręgu kąt o mierze \(\alpha\) (zobacz rysunek).
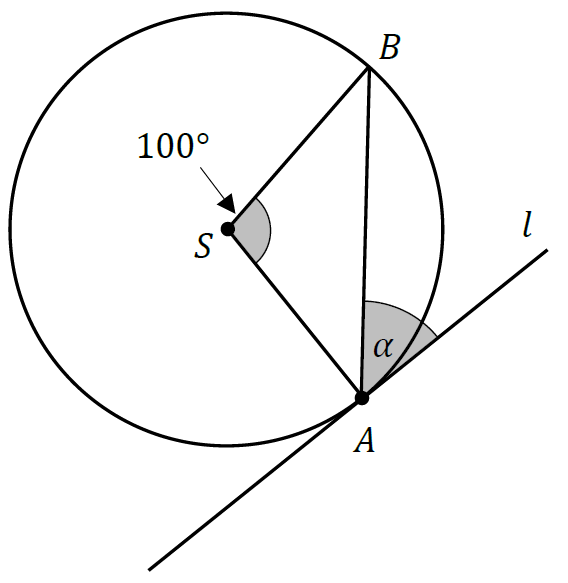
Wtedy:
A \(\alpha=40°\)
B \(\alpha=45°\)
C \(\alpha=50°\)
D \(\alpha=60°\)
Rozwiązanie:
Krok 1. Obliczenie miary kąta \(SAB\).
Trójkąt \(ABS\) jest równoramienny (ramiona są promieniami okręgu), w którym podstawą jest bok \(AB\). W takich trójkątach kąty przy podstawie mają jednakową miarę, więc skoro kąt między ramionami ma \(100°\), to na dwa pozostałe kąty zostaje nam \(180°-100°=80°\). To oznacza, że każdy z kątów przy podstawie ma \(80°:2=40°\).
Krok 2. Obliczenie miary kąta \(\alpha\).
Styczna do okręgu zawsze tworzy z promieniem okręgu kąt prosty. Skoro więc kąt \(SAB\) ma miarę \(40°\), to \(\alpha=90°-40°=50°\).
Teoria:
W trakcie opracowania
matura poprawkowa - CKE

