Wierzchołki \(A, B, C\) czworokąta \(ABSC\) leżą na okręgu o środku \(S\). Kąt \(ABS\) ma miarę \(40°\) (zobacz rysunek), a przekątna \(BC\) jest dwusieczną tego kąta.





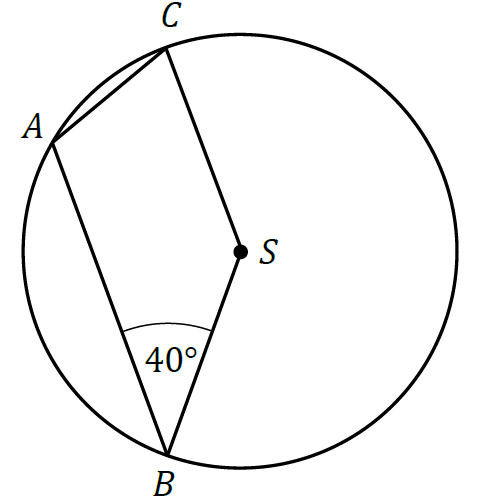
Miara kąta \(ASC\) jest równa:

A \(30°\)
B \(40°\)
C \(50°\)
D \(60°\)

Odpowiedź:      

B

Rozwiązanie:      
Krok 1. Obliczenie miary kąta BSC. Skoro przekątna \(BC\) jest dwusieczną kąta, to kąt \(ABC\) będzie miał miarę \(20°\). Tym samym powstanie nam taka oto sytuacja: Krok 2. Obliczenie miary kąta \(ASC\). Kąt \(ASC\) jest kątem środkowym, który oparty jest na tym samym łuku co znany nam kąt wpisany o mierze \(20°\). To oznacza, że miara tego kąta będzie dwa razy większa, czyli: $$|\sphericalangle ASC|=2\cdot20°=40°$$

Teoria:      
W trakcie opracowania