Zbiory arkuszy maturalnych z matematyki. Nasza strona oferuje bogaty wybór przykładowych arkuszy, rozwiązań zadań, testów z matematyki oraz wiele innych materiałów
Matura z matematyki (poziom podstawowy) - Maj 2023 (stara matura - formuła 2015) Zadanie 17 z 36
Zadanie nr 17. (1pkt)
W kartezjańskim układzie współrzędnych \((x,y)\) zaznaczono kąt \(\alpha\) o wierzchołku w punkcie \(O=(0;0)\). Jedno z ramion tego kąta pokrywa się z dodatnią półosią \(Ox\), a drugie przechodzi przez punkt \(P=(-3;1)\) (zobacz rysunek).
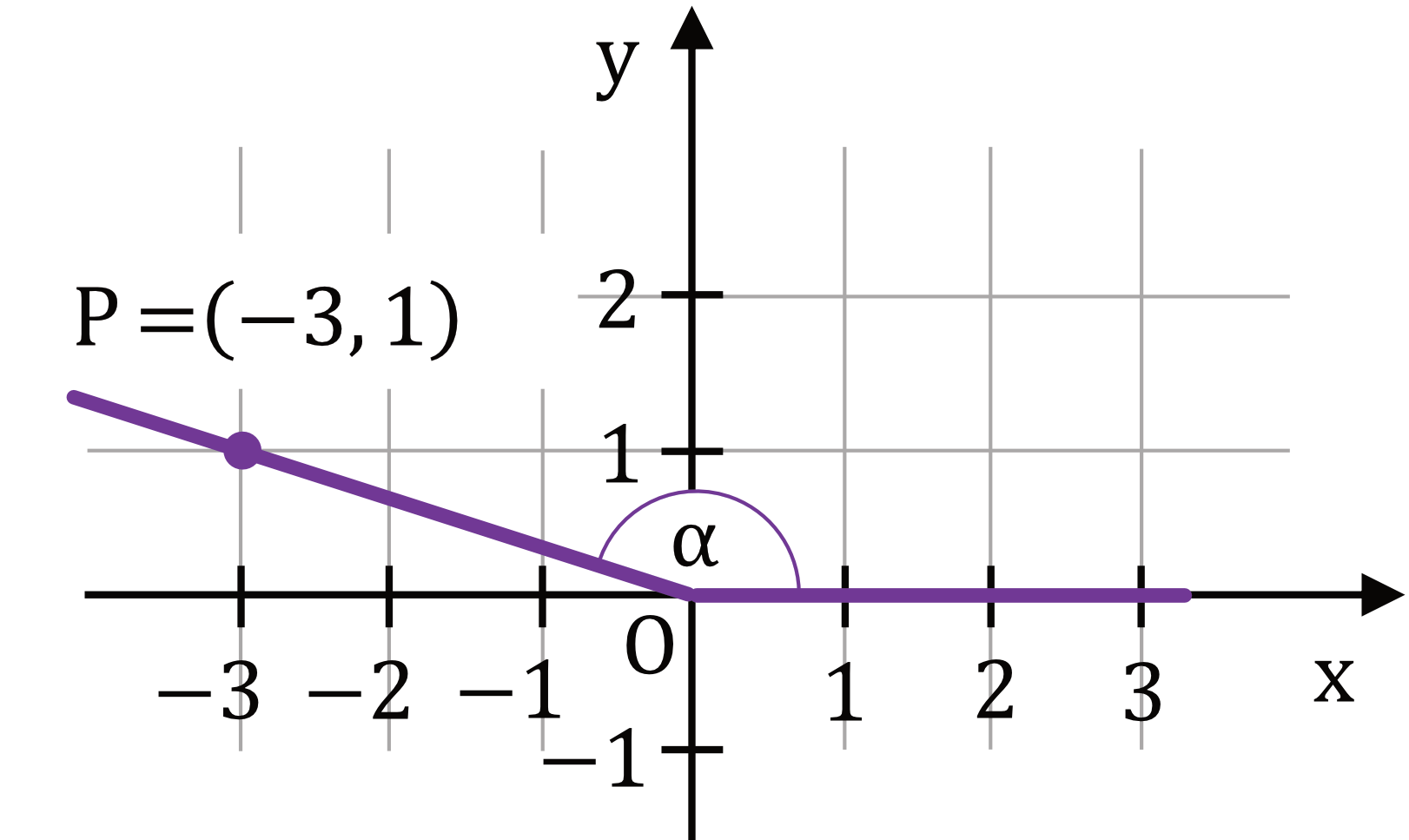
Tangens kąta \(\alpha\) jest równy:
A \(\frac{1}{\sqrt{10}}\)
B \(\left(-\frac{3}{\sqrt{10}}\right)\)
C \(\left(-\frac{3}{1}\right)\)
D \(\left(-\frac{1}{3}\right)\)
Rozwiązanie:
Opisana w zadaniu sytuacja jest bardzo charakterystyczna i związana jest tak naprawdę z definicjami funkcji trygonometrycznych. Możemy się tutaj posłużyć wzorami z tablic matematycznych, z których wynika, że:
$$tg\alpha=\frac{y}{x}$$
\(x\) oraz \(y\) to współrzędne punktu, przez który przechodzi drugie ramię kąta, zatem możemy zapisać, że:
$$tg\alpha=\frac{1}{-3}=-\frac{1}{3}$$
Teoria:
W trakcie opracowania
stara matura (formuła 2015) - CKE

