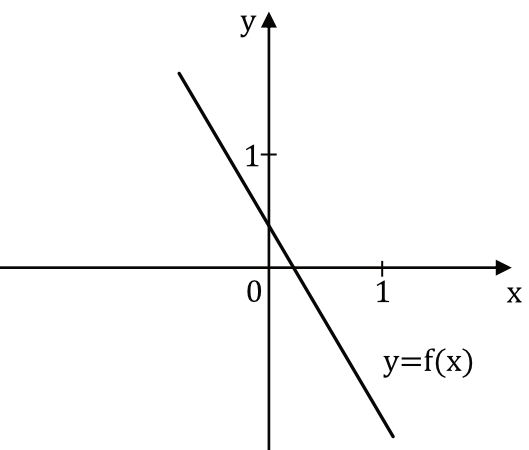Funkcja liniowa \(f\) jest określona wzorem \(f(x)=ax+b\), gdzie \(a\) i \(b\) są pewnymi liczbami rzeczywistymi. Na rysunku obok przedstawiono fragment wykresu funkcji \(f\) w kartezjańskim układzie współrzędnych (x,y).





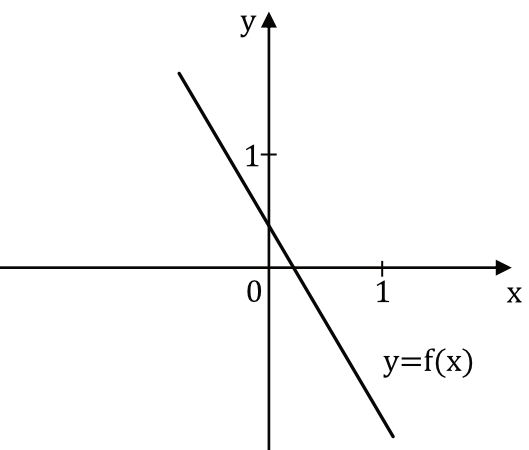
Liczba \(a\) oraz \(b\) we wzorze funkcji \(f\) spełniają warunki:

A \(a\gt0\) i \(b\gt0\)
B \(a\gt0\) i \(b\lt0\)
C \(a\lt0\) i \(b\gt0\)
D \(a\lt0\) i \(b\lt0\)

Odpowiedź:      

C

Rozwiązanie:      
Widzimy, że nasza funkcja jest malejąca, zatem współczynnik kierunkowy \(a\) musi być ujemny. To oznacza, że \(a\lt0\). Dodatkowo widzimy, że wykres funkcji przecina oś \(OY\) w dodatnim miejscu, a to prowadzi nas do wniosku, że współczynnik \(b\) jest dodatni, czyli \(b\gt0\). To oznacza, że liczby \(a\) oraz \(b\) spełniają warunki \(a\lt0\) i \(b\gt0\).

Teoria:      
W trakcie opracowania