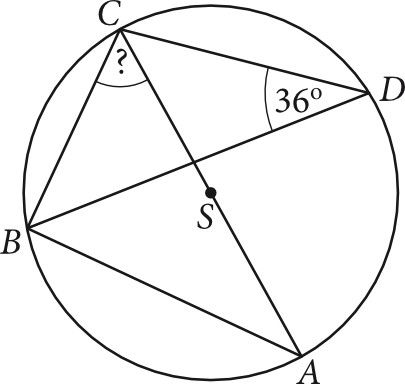
Punkty \(A, B, C, D\) są położone na okręgu o środku \(S\) tak, jak przedstawiono na rysunku. Odcinek \(AC\) jest średnicą tego okręgu. Wskaż miarę kąta \(BCA\).

A \(18°\)
B \(36°\)
C \(54°\)
D \(72°\)

Odpowiedź:      

C

Rozwiązanie:      
Krok 1. Dostrzeżenie trójkąta prostokątnego. Jeżeli odcinek \(AC\) jest średnicą okręgu, to z własności trójkątów wpisanych w okręg możemy wywnioskować, że trójkąt \(ABC\) jest trójkątem prostokątnym. Krok 2. Wyznaczenie miary kąta \(BAC\). Kąt \(BAC\) jest kątem wpisanym, który jest oparty na tym samym łuku co znany nam kąt \(BDC\). Skoro tak, to z własności takich trójkątów wynika, że będą miały one równą miarę, stąd też: $$|\sphericalangle BAC|=|\sphericalangle BDC|=36°$$ Krok 3. Obliczenie miary kąta \(BCA\). Spójrzmy na trójkąt \(ABC\). Znamy już dwie miary kątów w tym trójkącie, czyli \(|\sphericalangle CBA|=90°\) oraz \(|\sphericalangle BAC|=36°\). W związku z tym miara kąta \(BCA\) będzie równa: $$|\sphericalangle BCA|=180°-90°-36°=54°$$

Teoria:      
W trakcie opracowania