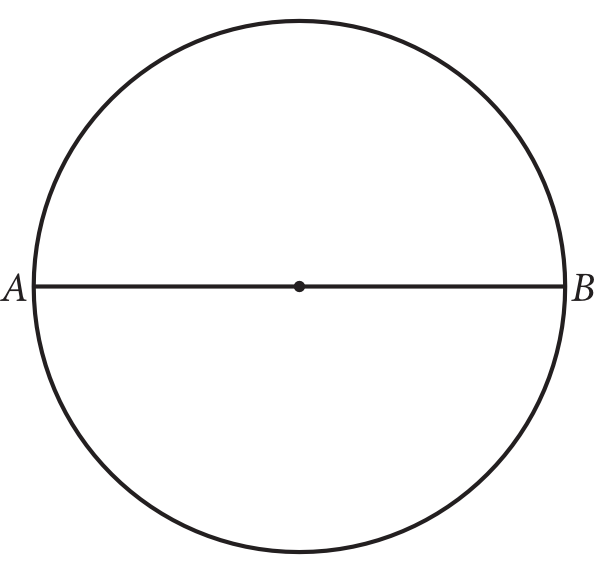
Odcinek \(AB\) jest średnicą koła (rysunek obok). Na jednym z łuków \(AB\) zaznaczono punkty \(C\), \(D\) i \(E\) różne od \(A\) i \(B\). W ten sposób powstały łuki \(AC, CD, DE, EB\), których długości są w stosunku \(1:1:2:4\). Miary kątów \(ACB\), \(ADB\) i \(AEB\) spełniają zależności:

A \(|\sphericalangle ACB|\lt|\sphericalangle ADB|\lt|\sphericalangle AEB|\)
B \(|\sphericalangle ACB|=|\sphericalangle ADB|=|\sphericalangle AEB|\)
C \(|\sphericalangle ACB|=|\sphericalangle ADB|\lt|\sphericalangle AEB|\)
D \(|\sphericalangle ACB|\lt|\sphericalangle ADB|=|\sphericalangle AEB|\)

Odpowiedź:      

B

Rozwiązanie:      
Krok 1. Sporządzenie rysunku pomocniczego. Zaznaczmy punkty \(C\), \(D\) i \(E\) w taki sposób, aby otrzymać odpowiedni stosunek długości łuków. Krok 2. Wybór prawidłowej odpowiedzi. Na rysunku powstały nam trzy trójkąty, które są oparte na średnicy okręgu. Z własności takich trójkątów wynika, że będą to trójkąty prostokątne, a kąty \(α, β, γ\) są właśnie kątami prostymi. Możemy więc powiedzieć, że każdy z wymienionych w zadaniu kątów ma jednakową miarę i będzie to \(90°\).

Teoria:      
W trakcie opracowania