Wskaż liczby, które należy wpisać do tabeli, aby wielkości \(x\) i \(y\) były odwrotnie proporcjonalne.

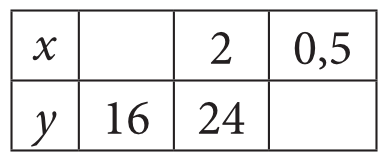
A \(x=6,\;y=22,5\)
B \(x=\frac{4}{3},\;y=6\)
C \(x=3,\;y=96\)
D \(x=4,\;y=1\)

Odpowiedź:      

C

Rozwiązanie:      
Krok 1. Wyznaczenie brakującej wartości \(x\). Wartości odwrotnie proporcjonalne charakteryzują się tym, że wraz z np. dwukrotnym wzrostem jednej liczby, spada dwukrotnie wartość drugiej liczby. Spójrzmy teraz na naszą tabelkę. Widzimy, że \(y_{1}=16\) oraz \(y_{2}=24\). Możemy więc dostrzec, że wartość igreka wzrosła półtorakrotnie, bo \(\frac{y_{2}}{y_{1}}=\frac{24}{16}=1,5\). To oznacza, że \(x_{2}\) powinno być \(1,5\) razy mniejsze od \(x_{1}\) lub też jak kto woli, \(x_{1}\) powinno być \(1,5\) razy większe od \(x_{2}\). Skoro \(x_{2}=2\), to \(x_{1}=1,5\cdot2=3\). Krok 2. Wyznaczenie brakującej wartości \(y\). Spójrzmy teraz na wartości \(x_{2}\) oraz \(x_{3}\). Widzimy, że \(x_{3}\) jest czterokrotnie mniejsze od \(x_{2}\), zatem \(y_{3}\) musi być czterokrotnie większe od \(y_{2}\). W związku z tym \(y_{3}=4\cdot24=96\). Tak na marginesie, to warto zauważyć, że iloczyn liczb w każdej kolumnie daje tą samą wartość: $$3\cdot16=48 \           ,\ 2\cdot24=48 \           ,\ 0,5\cdot96=48$$ To też może być dla nas wskazówka do rozwiązywania takich zadań lub chociażby weryfikowania poprawności obliczeń.

Teoria:      
W trakcie opracowania