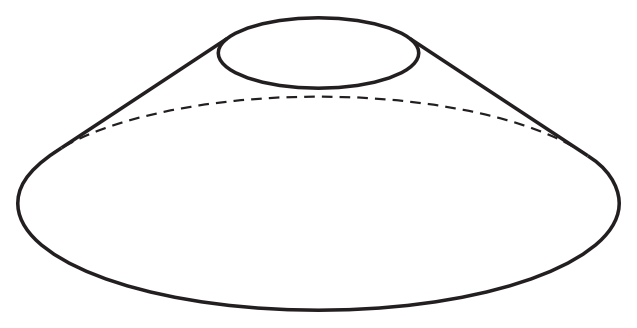
Objętość stożka ściętego (rysunek obok) dana jest wzorem \(V=\frac{1}{3}πH(r^2+rR+R^2)\), gdzie \(H\) jest wysokością bryły, a \(r\) i \(R\) są promieniami jej podstaw. Dane są: \(V=52π\), \(r=2\), \(R=6\). Wysokość bryły jest równa:

A \(\frac{13}{7}\)
B \(\frac{39}{7}\)
C \(1\)
D \(3\)

Odpowiedź:      

D

Rozwiązanie:      
Naszym zadaniem jest tak naprawdę podstawienie danych do wskazanego wzoru. Całość będzie wyglądać w następujący sposób: $$V=\frac{1}{3}πH(r^2+rR+R^2) \           ,\ 52π=\frac{1}{3}πH\cdot(2^2+2\cdot6+6^2) \           ,\ 52=\frac{1}{3}H\cdot(4+12+36) \           ,\ 52=\frac{1}{3}H\cdot52 \           ,\ \frac{1}{3}H=1 \           ,\ H=3$$

Teoria:      
W trakcie opracowania