Dany jest wielomian \(W(x)=x^3-4x^2+x+6\), gdzie \(x\in R\).



Dokończ zdanie tak, aby było prawdziwe. Wybierz odpowiedź A albo B oraz jej uzasadnienie spośród 1., 2. albo 3.



Wielomian \(W(x)\) jest podzielny przez:

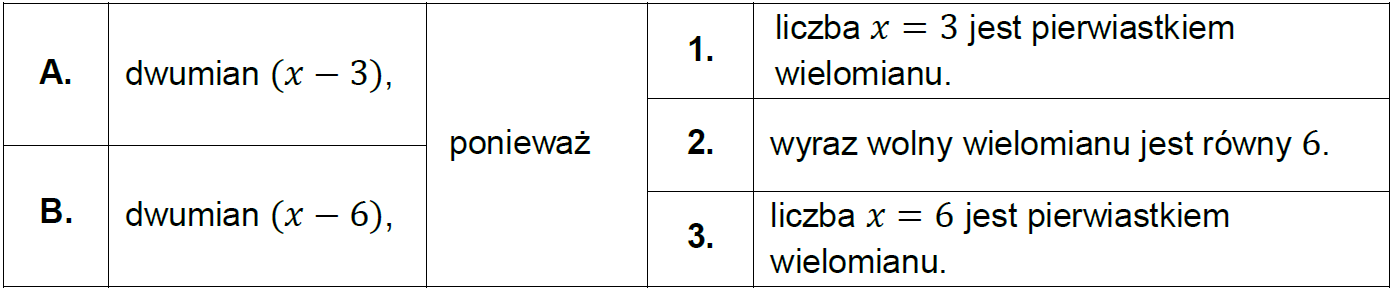
Odpowiedź:      

A., ponieważ 1.

Rozwiązanie:      
Wielomian jest podzielny przez dwumian typu \((x-a)\) wtedy, gdy \(W(a)=0\). Mówiąc bardzo obrazowo, musimy podstawić do wielomianu \(x=3\) oraz \(x=6\) i sprawdzić, kiedy otrzymamy wartość równą \(0\). W związku z tym: $$W(3)=3^3-4\cdot3^2+3+6 \           ,\ W(3)=27-4\cdot9+9 \           ,\ W(3)=27-36+9 \           ,\ W(3)=0$$ $$W(6)=6^3-4\cdot6^2+6+6 \           ,\ W(6)=216-4\cdot36+12 \           ,\ W(6)=216-144+12 \           ,\ W(6)=84$$ To oznacza, że wielomian jest podzielny przez dwumian \((x-3)\), ponieważ liczba \(x=3\) jest pierwiastkiem wielomianu.

Teoria:      
W trakcie opracowania