Na osi liczbowej zaznaczono sumę przedziałów.





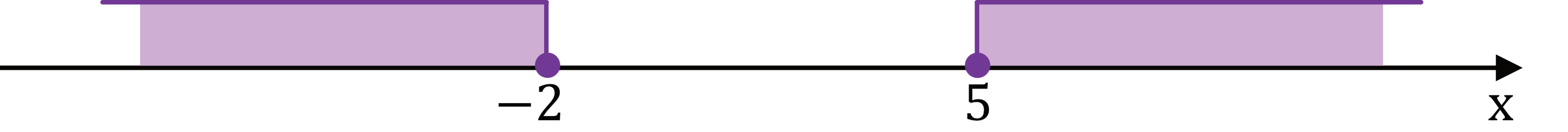
Zbiór zaznaczony na osi jest zbiorem wszystkich rozwiązań nierówności:

A \(|x-3,5|\ge1,5\)
B \(|x-1,5|\ge3,5\)
C \(|x-3,5|\le1,5\)
D \(|x-1,5|\le3,5\)

Odpowiedź:      

B

Rozwiązanie:      
Najbezpieczniejszym sposobem byłoby rozwiązywanie każdej z podanych nierówności z wartością bezwzględną. Jeśli jednak mamy trochę wprawy w rozwiązywaniu takich nierówności, to nasz wzrok powinien kierować się przede wszystkim ku odpowiedziom A oraz B. Dlaczego? Wynik będący sumą przedziałów jest charakterystyczny dla nierówności w których występuje znak typu \(\ge\). Gdybyśmy mieli jeden przedział, to wtedy interesowałyby nas w pierwszej kolejności nierówności ze znakiem typu \(\le\). Spróbujmy zatem rozwiązać podane nierówności: Odp. A. $$|x-3,5|\ge1,5 \           ,\ x-3,5\ge1,5 \quad\lor\quad x-3,5\le-1,5 \           ,\ x\ge5 \quad\lor\quad x\le2$$ Odp. B. $$|x-1,5|\ge3,5 \           ,\ x-1,5\ge3,5 \quad\lor\quad x-1,5\le-3,5 \           ,\ x\ge5 \quad\lor\quad x\le-2$$ Odp. C. $$|x-3,5|\le1,5 \           ,\ x-3,5\le1,5 \quad\land\quad x-3,5\ge-1,5 \           ,\ x\le5 \quad\land\quad x\ge2$$ Odp. D. $$|x-1,5|\le3,5 \           ,\ x-1,5\le3,5 \quad\land\quad x-1,5\ge-3,5 \           ,\ x\le5 \quad\land\quad x\ge-2$$ Interesujące nas rozwiązanie znalazło się zatem w drugiej nierówności.

Teoria:      
W trakcie opracowania