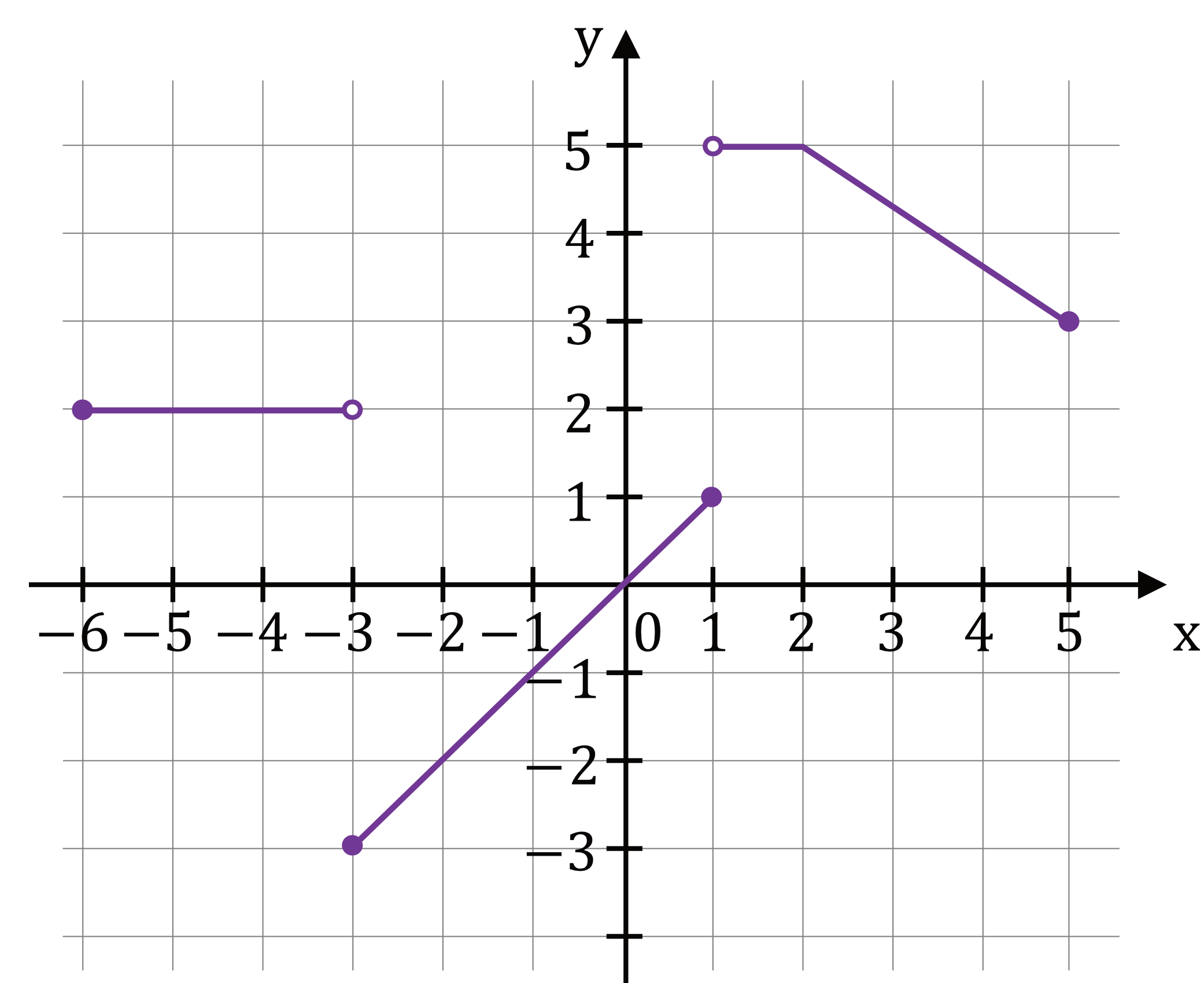
W kartezjańskim układzie współrzędnych \((x,y)\) narysowano wykres funkcji \(y=f(x)\) (zobacz rysunek)





Zadanie 1.

Dziedziną funkcji \(f\) jest zbiór:

A. \(\langle-6;5\rangle\)

B. \((-6;5)\)

C. \((-3;5\rangle\)

D. \(\langle-3;5\rangle\)



Zadanie 2.

Największa wartość funkcji \(f\) w przedziale \(\langle-4;1\rangle\) jest równa:

A. \(0\)

B. \(1\)

C. \(2\)

D. \(5\)



Zadanie 3.

Funkcja \(f\) jest malejąca w zbiorze:

A. \(\langle-6;-3)\)

B. \(\langle-3;1\rangle\)

C. \((1;2\rangle\)

D. \(\langle2;5\rangle\)

Odpowiedź:      

1. A
2. C
3. D

Rozwiązanie:      
Rozwiązanie 1. Dziedzinę funkcji odczytujemy z osi \(OX\). Widzimy, że funkcja przyjmuje wartości dla argumentów od \(x=6\) (włącznie z tym argumentem, bo kropka jest zamalowana), aż do \(x=5\) (także z tym argumentem, bo kropka zamalowana). To prowadzi nas do wniosku, że dziedziną funkcji \(f\) jest zbiór \(\langle-6;5\rangle\). Rozwiązanie 2. Spoglądając na wykres możemy stwierdzić, że w przedziale \(\langle-4;1\rangle\) największą przyjmowaną wartością jest \(y=2\). Rozwiązanie 3. Widzimy, że funkcja maleje od argumentu \(x=2\) aż do argumentu \(x=5\), więc moglibyśmy zapisać, że funkcja maleje dla argumentów \(x\) należących do zbioru \(\langle2;5\rangle\).

Teoria:      
W trakcie opracowania