Punkt kratowy to miejsce przecięcia się linii kwadratowej siatki. Pole wielokąta, którego wierzchołki znajdują się w punktach kratowych kwadratowej siatki na płaszczyźnie, można obliczyć ze wzoru Picka:

$$P=W+\frac{1}{2}B-1$$



gdzie \(P\) oznacza pole wielokąta, \(W\) – liczbę punktów kratowych leżących wewnątrz wielokąta, a \(B\) – liczbę punktów kratowych leżących na brzegu tego wielokąta.





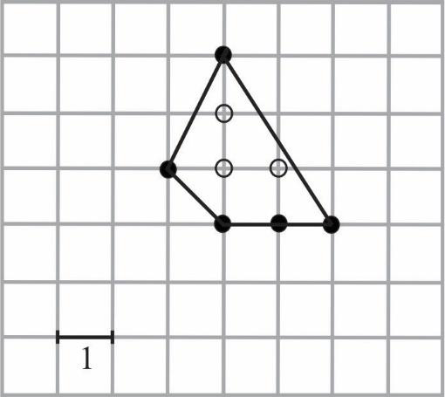
W wielokącie przedstawionym na rysunku \(W=3\) oraz \(B=5\), zatem \(P=4,5\).



Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami \(\bbox[5px,border:1px solid]{A}\) i \(\bbox[5px,border:1px solid]{B}\) oraz odpowiedź spośród oznaczonych literami \(\bbox[5px,border:1px solid]{C}\) i \(\bbox[5px,border:1px solid]{D}\).



Wielokąt, którego pole jest równe \(15\), może mieć \(\bbox[5px,border:1px solid]{A}\bigg/\bbox[5px,border:1px solid]{B}\) punktów kratowych leżących na brzegu wielokąta. Pole wielokąta, który ma dwukrotnie więcej punktów kratowych leżących na brzegu wielokąta niż punktów leżących wewnątrz, wyraża się liczbą \(\bbox[5px,border:1px solid]{C}\bigg/\bbox[5px,border:1px solid]{D}\).

A \(7\)
B \(8\)
C parzystą
D nieparzystą

Odpowiedź:      

B, D

Rozwiązanie:      
Krok 1. Rozwiązanie pierwszej części zadania. Spójrzmy na podany w treści zadania wzór, a konkretnie na zawarty w nim jednomian \(\frac{1}{2}B\). Gdybyśmy na brzegu wielokąta mieli \(7\) punktów, to z tego jednomianu wyszedłby nam ułamek \(\frac{1}{2}\cdot7=3,5\) i właśnie przez tę "połówkę" nie byłoby możliwości uzyskania w jakikolwiek sposób wyniku równego \(15\). Kiedy na brzegu będzie \(8\) wierzchołków (lub jakaś inna liczba parzysta), wtedy wynik \(15\) będzie możliwy do osiągnięcia, bo otrzymamy wartość całkowitą - w tym przypadku \(\frac{1}{2}\cdot8=4\). Dlatego też nasz poszukiwany wielokąt nie może mieć \(7\) punktów kratowych na brzegu, ale może mieć tych punktów \(8\). Krok 2. Rozwiązanie drugiej części zadania. Załóżmy sobie, że punktów wewnętrznych mamy \(W=n\) natomiast punktów brzegowych mamy \(B=2n\) (bo ma być ich dwa razy więcej niż wewnętrznych). Podstawiając to do wzoru otrzymamy: $$P=n+\frac{1}{2}2n-1 \           ,\ P=n+n-1 \           ,\ P=2n-1$$ Jakiejkolwiek liczby nie podstawimy pod \(n\) to otrzymane wyrażenie da nam liczbę nieparzystą. Oczywiście można też wykorzystać fakt, że jest to zadanie zamknięte i podstawić sobie jakieś przykładowe liczby i sprawdzić jaki otrzymamy wynik. Przykładowo: Gdy \(W=5\) oraz \(B=10\), to: $$P=5+\frac{1}{2}\cdot10-1 \           ,\ P=5+5-1 \           ,\ P=9$$ Otrzymany wynik jest nieparzysty.

Teoria:      
W trakcie opracowania