Przekątne prostokąta \(ABCD\) przedstawionego na rysunku przecinają się pod kątem \(140°\).





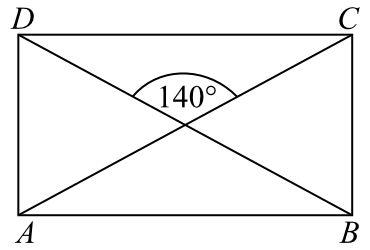
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe. Kąt \(DCA\) ma miarę \(40°\).
Kąt \(DAC\) ma miarę \(70°\).

Kąt \(DCA\) ma miarę \(40°\).

Odpowiedź:      

1) FAŁSZ

2) PRAWDA

Rozwiązanie:      
Oznaczmy sobie miejsce przecięcia się przekątnych jako punkt \(S\). Krok 1. Ocena prawdziwości pierwszego zdania. Spójrzmy na trójkąt \(DCS\). Jest to trójkąt równoramienny o podstawie \(DC\). W trójkącie równoramiennym kąty przy podstawie mają równą miarę, zatem kąt \(DCA\) (lub też \(DCS\)) ma miarę: $$|\sphericalangle DCA|=(180°-140°):2 \           ,\ |\sphericalangle DCA|=40°:2 \           ,\ |\sphericalangle DCA|=20°$$ Zdanie jest więc fałszem. Krok 2. Ocena prawdziwości drugiego zdania. Korzystając z własności kątów przyległych możemy zapisać, że: $$|\sphericalangle ASD|=180°-140°=40°$$ Trójkąt \(ADS\) jest także trójkątem równoramiennym o podstawie \(AD\), zatem kąty przy podstawie (w tym intresujący nas kąt \(DAC\)) ma miarę: $$|\sphericalangle DAC|=(180°-40°):2 \           ,\ |\sphericalangle DAC|=140°:2 \           ,\ |\sphericalangle DAC|=70°$$ Zdanie jest więc prawdą.

Teoria:      
W trakcie opracowania