Prosta \(EF\) dzieli prostokąt \(ABCD\) na kwadrat \(EFCD\) o obwodzie \(32cm\) i prostokąt \(ABFE\) o obwodzie o \(6cm\) mniejszym od obwodu kwadratu \(EFCD\).





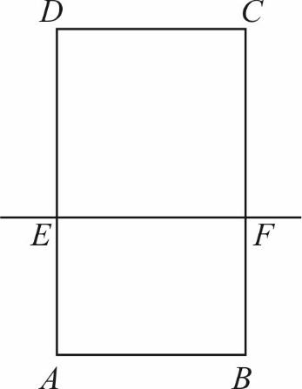
Długość odcinka \(AE\) jest równa:

A \(2cm\)
B \(4cm\)
C \(5cm\)
D \(8cm\)

Odpowiedź:      

C

Rozwiązanie:      
Krok 1. Obliczenie długości boku kwadratu \(EFCD\). Wiemy, że kwadrat \(EFCD\) ma obwód równy \(32cm\). Kwadrat ma wszystkie boki równej długości, zatem każdy bok tego kwadratu ma długość: $$32cm:4=8cm$$ Krok 2. Obliczenie obwodu prostokąta \(ABFE\). Wiemy, że prostokąt \(ABFE\) ma obwód o \(6cm\) mniejszy od kwadratu, zatem: $$Obw_{ABFE}=32cm-6cm=26cm$$ Krok 3. Obliczenie długości odcinka \(AE\). Spójrzmy na prostokąt \(ABFE\). Z kroku pierwszego wiemy, że \(EF=8cm\), zatem także \(AB=8cm\). Te dwa boki prostokąta mają więc razem \(8cm+8cm=16cm\). To oznacza, że na pozostałe boki prostokąta \(ABFE\), czyli na boki \(AE\) oraz \(BF\), zostaje nam \(26cm-16cm=10cm\). Te dwa boki prostokąta są oczywiście równej miary, zatem każdy z nich ma długość \(10cm:2=5cm\).

Teoria:      
W trakcie opracowania