Punkt kratowy to miejsce przecięcia się linii kwadratowej siatki. Pole wielokąta, którego wierzchołki znajdują się w punktach kratowych kwadratowej siatki na płaszczyźnie, można obliczyć ze wzoru Picka:

$$P=W+\frac{1}{2}B-1$$



gdzie \(P\) oznacza pole wielokąta, \(W\) – liczbę punktów kratowych leżących wewnątrz wielokąta, a \(B\) – liczbę punktów kratowych leżących na brzegu tego wielokąta.





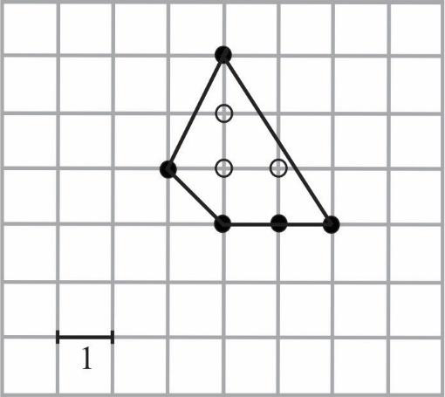
W wielokącie przedstawionym na rysunku \(W=3\) oraz \(B=5\), zatem \(P=4,5\). Wewnątrz pewnego wielokąta znajduje się \(5\) punktów kratowych, a na jego brzegu jest \(6\) punktów kratowych. Pole tego wielokąta jest równe:

A \(6\)
B \(6,5\)
C \(7\)
D \(7,5\)

Odpowiedź:      

C

Rozwiązanie:      
Korzystając z podanego wzoru możemy zapisać, że: $$P=5+\frac{1}{2}\cdot6-1 \           ,\ P=5+3-1 \           ,\ P=7$$

Teoria:      
W trakcie opracowania