Na bokach trójkąta prostokątnego \(ABC\) zaznaczono punkty \(D\) i \(E\). Odcinek \(DE\) podzielił trójkąt \(ABC\) na dwa wielokąty: trójkąt prostokątny \(ADE\) i czworokąt \(DBCE\), jak na rysunku. Odcinek \(AB\) ma długość \(4\sqrt{3}cm\), a odcinek \(DE\) ma długość \(3cm\).





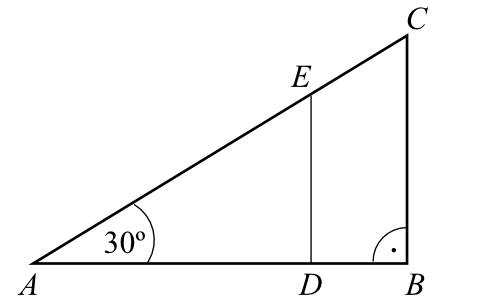
Długość odcinka \(EC\) jest równa:

A \(1cm\)
B \(\sqrt{3}cm\)
C \(2cm\)
D \(4cm\)
E \(3\sqrt{3}cm\)

Odpowiedź:      

C

Rozwiązanie:      
Krok 1. Obliczenie długości odcinka \(AC\). Spójrzmy na duży trójkąt \(ABC\). Skorzystamy tutaj z własności trójkątów o kątach \(30°, 60°, 90°\). Z tych własności wynika, że przyprostokątna leżąca przy kącie \(30°\) (czyli nasz odcinek \(AB\)) ma długość \(a\sqrt{3}\), druga przyprostokątna (czyli nasz odcinek \(BC\)) ma długość \(a\), natomiast przeciwprostokątna (czyli nasz odcinek \(AC\)) ma długość \(2a\). Skoro odcinek \(AB\) ma długość \(4\sqrt{3}cm\), to możemy zapisać że: $$a\sqrt{3}cm=4\sqrt{3}cm \           ,\ a=4cm$$ W związku z tym przeciwprostokątna \(AC\) ma długość: $$|AC|=2a \           ,\ |AC|=2\cdot4cm \           ,\ |AC|=8cm$$ Krok 2. Obliczenie długości odcinka \(AE\). Teraz spójrzmy na trójkąt \(ADE\). Tutaj także skorzystamy z własności trójkątów \(30°, 60°, 90°\). Tym razem znamy długość krótszej przyprostokątnej \(DE\), czyli możemy zapisać że \(a=3cm\). Nas interesuje długość odcinka \(AE\), czyli: $$|AE|=2a \           ,\ |AE|=2\cdot3cm \           ,\ |AE|=6cm$$ Krok 3. Obliczenie długości odcinka \(EC\). Odcinek \(EC\) jest różnicą między odcinkiem \(AC\) oraz odcinkiem \(AE\): $$|EC|=8cm-6cm \           ,\ |EC|=2cm$$

Teoria:      
W trakcie opracowania