Na stole leżą płytki w kształcie trójkątów równobocznych o bokach długości \(3cm\) i płytki kwadratowe, których boki także mają długość \(3cm\). Marysia ułożyła z nich figurę taką, jak na rysunku.





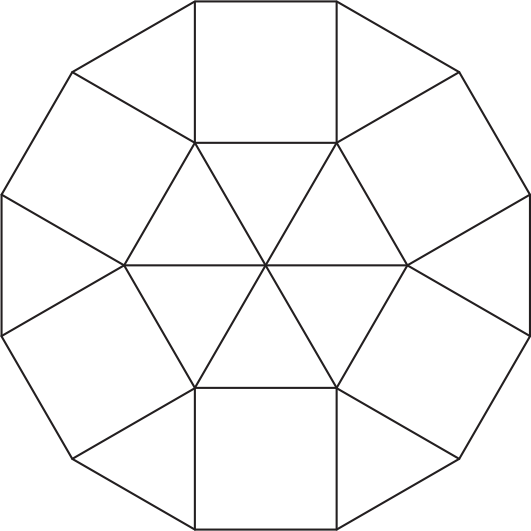
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F - jeśli jest fałszywe. Otrzymana figura to dwunastokąt foremny.
Łączna powierzchnia trójkątnych płytek jest większa niż łączna powierzchnia płytek kwadratowych.

Otrzymana figura to dwunastokąt foremny.

Odpowiedź:      

1) PRAWDA

2) FAŁSZ

Rozwiązanie:      
Krok 1. Ocena prawdziwości pierwszego zdania. To, że figura nasza jest dwunastokątem nie podlega raczej wątpliwości - wystarczy policzyć boki lub kąty. Pytanie jednak, czy jest to dwunastokąt foremny (czyli czy wszystkie boki są jednakowej długości). Jak najbardziej jest to dwunastokąt foremny, bo zarówno kwadraty jak i trójkąty równoboczne (z których zbudowana jest figura) mają krawędź o długości \(3cm\), czyli każdy bok naszego dwunastokąta ma długość \(3cm\). Zdanie jest więc prawdą. Krok 2. Ocena prawdziwości drugiego zdania. Aby się przekonać o tym, czy jest to prawda, musimy obliczyć pola powierzchni kwadratów i trójkątów. Zacznijmy od kwadratów. Z rysunku wynika, że mamy \(6\) kwadratów o boku \(3cm\). Pole pojedynczego kwadratu obliczamy ze wzoru \(P=a^2\), zatem skoro takich kwadratów mamy \(6\) to otrzymamy: $$P_{k}=6\cdot3^2 \           ,\ P_{k}=6\cdot9 \           ,\ P_{k}=54$$ Teraz obliczmy łączną powierzchnię trójkątów. Widzimy, że mamy \(12\) trójkątów równobocznych o boku \(3cm\). Pole każdego pojedynczego trójkąta możemy obliczyć ze wzoru \(P=\frac{a^2\sqrt{3}}{4}\), zatem łączne pole wszystkich trójkątów będzie równe: $$P_{t}=12\cdot\frac{3^2\sqrt{3}}{4} \           ,\ P_{t}=12\cdot\frac{9\sqrt{3}}{4} \           ,\ P_{t}=3\cdot9\sqrt{3} \           ,\ P_{t}=27\sqrt{3}$$ Jeżeli przyjmiemy, że \(\sqrt{3}\approx1,73\), to możemy wtedy zapisać, że \(P_{t}\approx27\cdot1,73\approx46,71\). To oznacza, że pole powierzchni trójkątów jest mniejsze od pola powierzchni kwadratów, zatem to zdanie jest fałszem.

Teoria:      
W trakcie opracowania