Suma długości wszystkich krawędzi ostrosłupa prawidłowego sześciokątnego jest równa \(450\). Krawędź boczna jest w tym ostrosłupie czterokrotnie dłuższa od krawędzi podstawy.





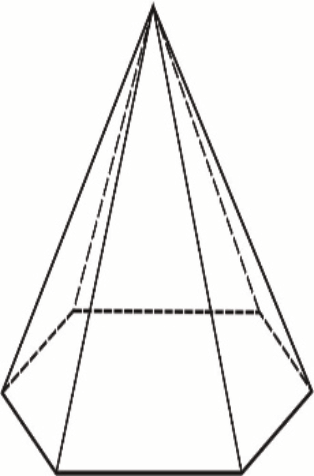
Długość krawędzi podstawy tego ostrosłupa jest równa:

A \(15\)
B \(25\)
C \(50\)
D \(60\)

Odpowiedź:      

A

Rozwiązanie:      
Krok 1. Wprowadzenie oznaczeń do treści zadania. Wprowadźmy do zadania następujące oznaczenia: \(x\) - długość krawędzi podstawy \(4x\) - długość krawędzi bocznej Krok 2. Obliczenie długości krawędzi podstawy. Ostrosłup prawidłowy sześciokątny będzie miał \(6\) krawędzi podstawy i \(6\) krawędzi bocznych. Suma tych krawędzi jest równa \(450\), zatem: $$6x+6\cdot4x=450 \           ,\ 6x+24x=450 \           ,\ 30x=450 \           ,\ x=15$$ Długość krawędzi podstawy tego ostrosłupa jest zatem równa \(15\).

Teoria:      
W trakcie opracowania