W trójkącie \(ABC\) o obwodzie \(34 cm\) poprowadzono odcinek \(DE\). Obwód trójkąta \(AED\) jest równy \(16 cm\), a obwód czworokąta \(EBCD\) - \(30 cm\).





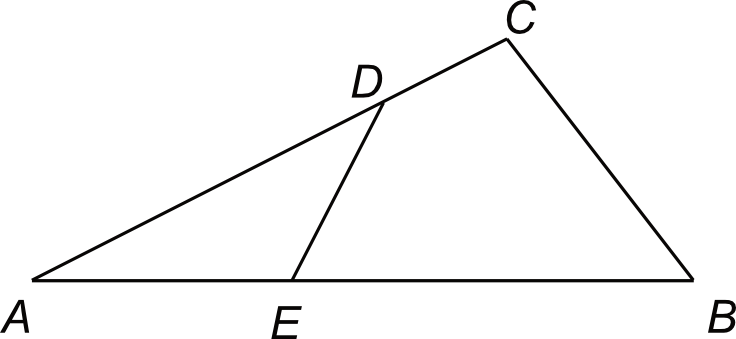
Długość odcinka \(DE\) jest równa:

A \(4 cm\)
B \(6 cm\)
C \(7 cm\)
D \(12 cm\)

Odpowiedź:      

B

Rozwiązanie:      
Musimy dobrze przeanalizować rysunek. Czym się różni suma obwodów trójkąta \(AED\) oraz czworokąta \(EBCD\), od obwodu trójkąta \(ABC\)? Różni się właśnie tylko tym odcinkiem \(DE\), którego długości szukamy. To właśnie na tej obserwacji oprzemy rozwiązania tego zadania. Suma obwodów trójkąta \(AED\) oraz czworokąta \(EBCD\) wynosi: $$Obw=16cm+30cm \           ,\ Obw=46cm$$ Skoro suma tych dwóch figur jest równa \(46cm\), a obwód trójkąta \(ABC\) wynosi \(34cm\), to różnica obwodów jest równa: $$46cm-34cm=12cm$$ Ale to nie koniec obliczeń. Pułapką w tym zadaniu jest fakt, że my ten odcinek \(DE\) policzyliśmy tak naprawdę podwójnie (raz w obwodzie trójkąta \(AED\) i raz w czworokącie \(EBCD\)). Skoro tak, to: $$|DE|=12cm:2=6cm$$

Teoria:      
W trakcie opracowania