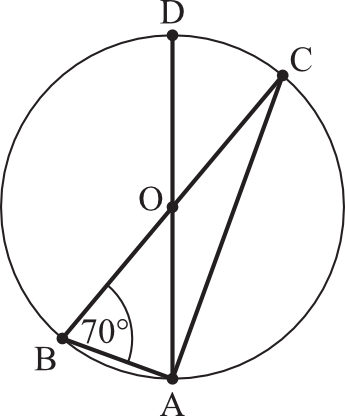
Punkty \(A,B,C,D\) należą do okręgu o środku \(O\). Jeśli kąt \(ABC\) ma miarę \(70°\), to kąt \(DAC\) ma miarę:

A \(70°\)
B \(50°\)
C \(40°\)
D \(20°\)

Odpowiedź:      

D

Rozwiązanie:      
Krok 1. Obliczenie miary kąta \(OAB\). Musimy zauważyć, że trójkąt \(ABO\) jest trójkątem równoramiennym - jego ramionami są długości promienia poprowadzone z punktu \(O\). Z własności trójkątów równoramiennych wynika, że kąty przy podstawie mają jednakową miarę, zatem: $$|\sphericalangle OAB|=70°$$ Krok 2. Obliczenie miary kąta \(BAC\). Teraz spójrzmy na trójkąt \(ABC\). Jest to trójkąt w którym jeden z boków pokrywa się ze średnicą okręgu. Skoro tak, to musi to być trójkąt prostokątny, zatem: $$|\sphericalangle BAC|=90°$$ Krok 3. Obliczenie miary kąta \(DAC\). Kąt \(DAC\) jest tak naprawdę różnicą między kątem prostym \(BAC\) oraz kątem \(OAB\), zatem: $$|\sphericalangle DAC|=|\sphericalangle BAC|-|\sphericalangle OAB| \           ,\ |\sphericalangle DAC|=90°-70° \           ,\ |\sphericalangle DAC|=20°$$

Teoria:      
W trakcie opracowania