Na rysunku przedstawiono fragment wykresu funkcji kwadratowej \(f\) określonej wzorem \(f(x)=2x^2+5x\).





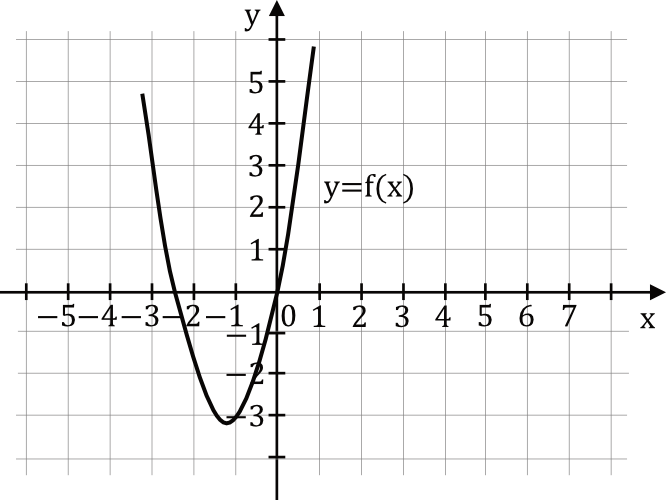
Osią symetrii wykresu funkcji \(f\) jest prosta o równaniu:

A \(x=-\frac{5}{4}\)
B \(x=\frac{5}{4}\)
C \(y=-\frac{5}{4}\)
D \(y=-\frac{25}{16}\)

Odpowiedź:      

A

Rozwiązanie:      
Oś symetrii wykresu funkcji kwadratowej na pewno przechodzi przez wierzchołek i jest równoległa do osi \(OY\). Trzeba byłoby więc poznać pierwszą współrzędną wierzchołka paraboli (zwyczajowo zapisywaną jako \(p\)). W tym celu możemy skorzystać ze wzoru: $$p=\frac{-b}{2a}$$ Podstawiając współczynniki \(a=2\) oraz \(b=5\), otrzymamy: $$p=\frac{-5}{2\cdot2} \           ,\ p=-\frac{5}{4}$$ Tak na marginesie - współrzędną \(p\) można było też próbować odczytać z rysunku. Widzimy, że współrzędna \(p\) wierzchołka paraboli przyjmuje wartość około \(p\approx-1\), a patrząc się na proponowane odpowiedzi jesteśmy w stanie wywnioskować, że \(p=-\frac{5}{4}\). To z kolei prowadzi nas do wniosku, że poszukiwaną osią symetrii będzie prosta o równaniu \(x=-\frac{5}{4}\).

Teoria:      
W trakcie opracowania