Na rysunku jest przedstawiona graficzna ilustracja układu dwóch równań stopnia pierwszego z dwiema niewiadomymi \(x\) i \(y\).





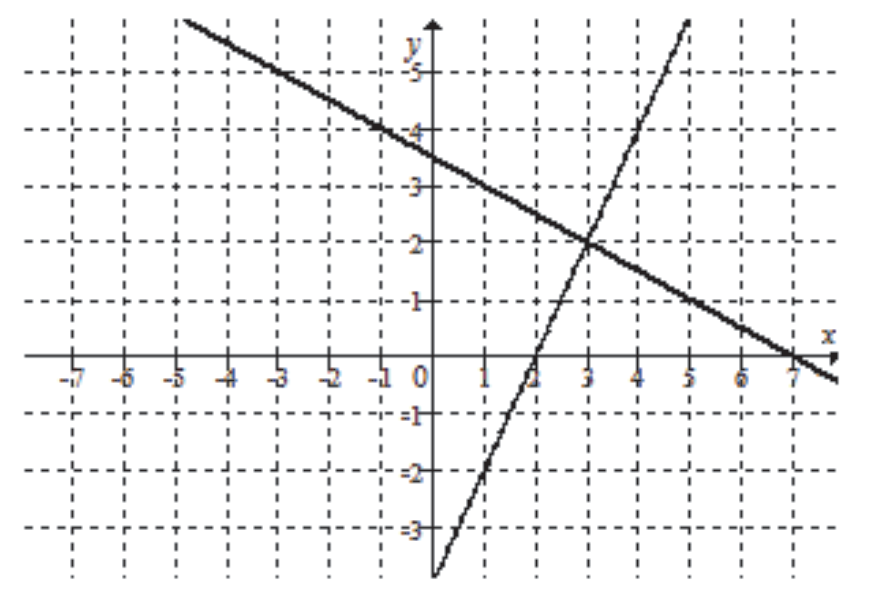
Wskaż ten układ.

A \(\begin{cases} y=-2x+8 \\ y=-\frac{3}{2}x+\frac{13}{2} \end{cases}\)
B \(\begin{cases} y=2x-4 \\ y=-\frac{1}{2}x+\frac{7}{2} \end{cases}\)
C \(\begin{cases} y=x-1 \\ y=\frac{1}{2}x+\frac{1}{2} \end{cases}\)
D \(\begin{cases} y=3x-7 \\ y=-\frac{2}{3}x+4 \end{cases}\)

Odpowiedź:      

B

Rozwiązanie:      
Z rysunku możemy odczytać, że jedna prosta jest rosnąca, a druga jest malejąca. To oznacza, że jedna z prostych musi mieć współczynnik kierunkowy \(a\) dodatni, a druga musi mieć ujemny. Ogranicza nam to wybór odpowiedzi do B oraz D. Pozostałe warianty możemy już odrzucić. Aby ustalić który układ równań jest tym dobrym wystarczy spojrzeć np. na miejsce przecięcia się prostej malejącej z osią igreków. Prosta ta przecina oś igreków dla \(x=3,5\), czyli \(x=\frac{7}{2}\). To oznacza, że współczynnik \(b\) tej prostej musi być równy właśnie \(b=\frac{7}{2}\). Taką sytuację mamy w odpowiedzi B.

Teoria:      
W trakcie opracowania