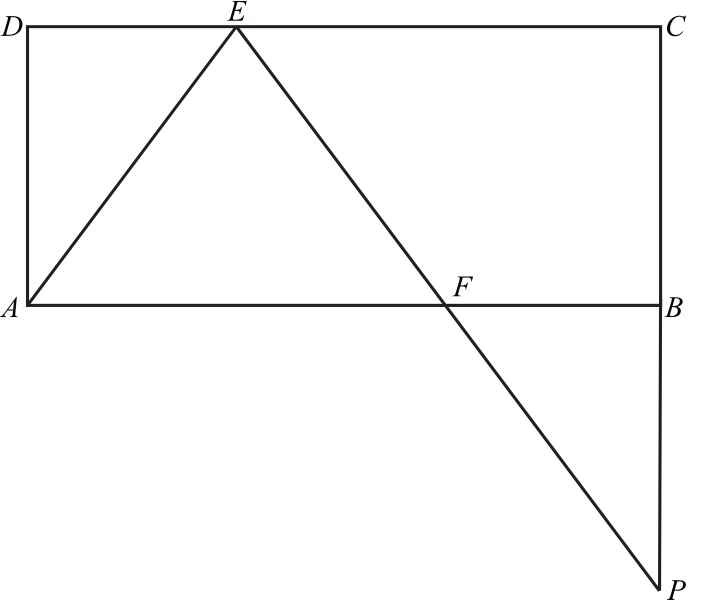
Dany jest prostokąt \(ABCD\). Na boku \(CD\) tego prostokąta wybrano taki punkt \(E\), że \(|EC|=2|DE|\), a na boku \(AB\) wybrano taki punkt \(F\), że \(|BF|=|DE|\). Niech \(P\) oznacza punkt przecięcia prostej \(EF\) z prostą \(BC\) (zobacz rysunek). Wykaż, że trójkąty \(AED\) i \(FPB\) są przystające.

Odpowiedź:      

Wykazano korzystając z podobieństwa trójkątów.

Rozwiązanie:      
Krok 1. Sporządzenie rysunku pomocniczego. Wprowadźmy na nasz rysunek pewne oznaczenia. Oznaczmy odcinek \(DE\) jako \(x\), a co za tym idzie odcinek \(EC\) jako \(2x\). Z treści zadania wynika, że odcinek \(BF\) jest równy odcinkowi \(DE\), czyli tutaj także mamy długość \(x\). Dodatkowo oznaczmy już inną niewiadomą boki \(AD\) oraz \(BC\), które mają jednakową miarę (niech to będzie niewiadoma \(y\)), no i niech kluczowy bok \(BP\) ma miarę \(z\). Naszym zadaniem jest udowodnienie, że trójkąty \(AED\) oraz \(FPB\) są przystające, a skoro mają taką samą podstawę równą \(x\) to musimy tak naprawdę udowodnić, że \(y=z\) (tylko wtedy będą to trójkąty przystające). Krok 2. Dostrzeżenie podobieństwa trójkątów \(PCE\) oraz \(PBF\). Trójkąty \(PCE\) oraz \(PBF\) są na pewno podobne (mają jednakowe miary kątów). Skoro więc trójkąt \(PCE\) ma podstawę równą \(2x\), a trójkąt \(PBF\) ma podstawę dwukrotnie mniejszą, bo równą \(x\), to znaczy że także odcinek \(PC\) musi być dwukrotnie dłuższy od odcinka \(PB\) (czyli skala podobieństwa jest równa \(2\)). Zatem: $$|PC|=2|PB| \           ,\ y+z=2z \quad\bigg/-z \           ,\ y=z$$ Krok 3. Zakończenie dowodzenia. Udało nam się w ten sposób udowodnić, że długość \(y\) jest równa długości \(z\). To oznacza, że trójkąty \(AED\) oraz \(FPB\) mają jednakowe długości przyprostokątnych, zatem i przeciwprostokątne muszą mieć tą samą długość. Skoro więc obydwa trójkąty mają boki jednakowych miar, to są to trójkąty przystające.

Teoria:      
W trakcie opracowania