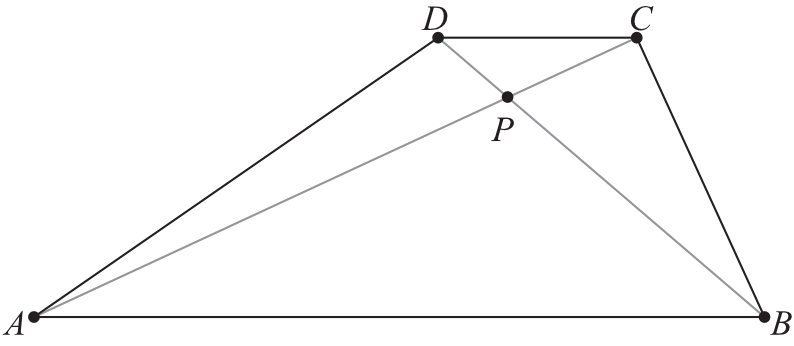
W trapezie \(ABCD\) przekątne przecinają się w punkcie \(P\). Punkt \(P\) dzieli przekątne na odcinki długości: \(|AP|=8\), \(|PC|=3\) i \(|BP|=12\). Długości podstaw \(AB\) i \(CD\) trapezu różnią się o \(15\). Oblicz długość odcinka \(DP\) oraz długości podstaw \(AB\) i \(CD\) trapezu.

Odpowiedź:      

\(|DP|=4,5\); \(|CD|=9\) oraz \(|AB|=24\)

Rozwiązanie:      
Krok 1. Dostrzeżenie trójkątów podobnych. W naszym trapezie trójkąty \(ABP\) oraz \(DCP\) są trójkątami podobnymi, bo mają one identyczne miary kątów (cecha kąt-kąt-kąt). Ogólnie warto pamiętać o tej własności trapezów, a wynika ona wprost z własności kątów naprzemianległych i wierzchołkowych: Aby łatwiej było dostrzec poszczególne zależności w trójkątach podobnych, to narysujmy sobie te dwa trójkąty obok siebie, zaznaczając przy okazji wymiary z treści zadania: Krok 2. Wyznaczenie długości odcinka \(DP\). Skoro trójkąty \(ABP\) oraz \(DCP\) są podobne to możemy ułożyć następującą proporcję: $$\frac{|BP|}{|DP|}=\frac{|AP|}{|CP|} \           ,\ \frac{12}{|DP|}=\frac{|8|}{|3|}$$ Mnożąc teraz na krzyż otrzymamy: $$12\cdot3=|DP|\cdot8 \           ,\ 8|DP|=36 \           ,\ |DP|=4,5$$ Krok 3. Obliczenie długości podstawy \(CD\). Ponownie korzystając z trójkątów podobnych i z informacji o tym, że podstawy \(AB\) oraz \(CD\) różnią się o \(15\) możemy zapisać, że: $$\frac{|AB|}{|CD|}=\frac{|AP|}{|CP|} \           ,\ \frac{x+15}{x}=\frac{8}{3}$$ Mnożąc na krzyż otrzymamy: $$(x+15)\cdot3|=x\cdot8 \           ,\ 3x+45=8x \           ,\ 45=5x \           ,\ x=9$$ To oznacza, że \(|CD|=9\). Krok 4. Obliczenie długości podstawy \(AB\). Podstawa \(AB\) jest o \(15\) dłuższa od podstawy \(CD\), zatem: $$|AB|=|CD|+15 \           ,\ |AB|=9+15 \           ,\ |AB|=24$$ Uwaga: To zadanie ma zaszyty w sobie pewien ciekawy błąd, bowiem taki trapez nie istnieje. Skąd to wiemy? Jak spojrzymy na trójkąt \(ABP\) to zauważymy, że jego boki mają długość \(24, 12, 8\). Taki trójkąt nie może istnieć, bo jedną z własności trójkątów jest to, że suma dwóch krótszych boków trójkąta musi być większa niż długość najdłuższego boku trójkąta. W naszym przypadku suma dwóch najkrótszych boków jest równa \(8+12=20\), czyli jest mniejsza od \(24\). To jest dowód na to, że trapez o wymiarach boków z treści zadania tak naprawdę nie istnieje.

Teoria:      
W trakcie opracowania