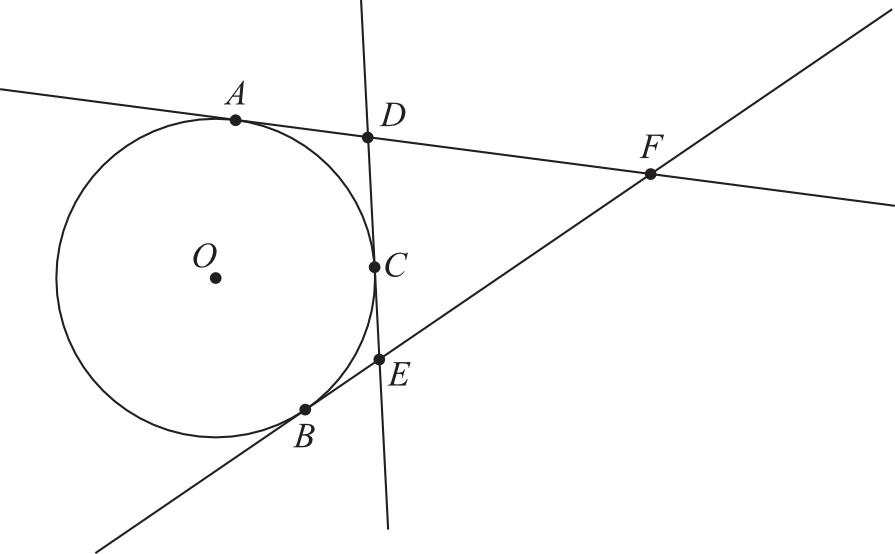
Do okręgu o środku w punkcie \(O\) poprowadzono z trzech punktów \(A\), \(B\) i \(C\) leżących na okręgu styczne, które przecięły się w punktach \(D\), \(E\) i \(F\) (zobacz rysunek). Wykaż, że jeżeli \(|AF|=x\), to obwód trójkąta \(DEF\) jest równy \(2x\).

Odpowiedź:      

Udowodniono korzystając z własności stycznych do okręgu.

Rozwiązanie:      
Krok 1. Dostrzeżenie odcinków o jednakowej długości. Z własności stycznych do okręgu powinniśmy zauważyć trzy pary boków o identycznych miarach: $$|DC|=|AD| \           ,\ |CE|=|BE| \           ,\ |AF|=|BF|$$ Krok 2. Rozpisanie długości obwodu trójkąta. Patrząc się na rysunek możemy zapisać, że obwód trójkąta będzie równy: $$Obw=|EF|+|DF|+|DC|+|CE|$$ W pierwszym kroku zapisaliśmy sobie, że odcinek \(DC\) ma taką samą miarę jak odcinek \(AD\) oraz że odcinek \(CE\) ma taką samą miarę jak odcinek \(BE\). Podmieniając te dwa odcinki w naszym powyższym zapisie otrzymamy: $$Obw=\color{green}{|EF|}+\color{blue}{|DF|+|AD|}+\color{green}{|BE|}$$ Teraz spójrzmy na nasze działanie. Z treści zadania wynika, że odcinek \(AF\) ma długość \(x\), a na odcinek \(AF\) składa się suma \(\color{blue}{|AD|+|DF|}\). Podobnie jest z odcinkiem \(BF\) na którego składa się suma \(\color{green}{|BE|+|EF|}\). To by oznaczało, że: $$Obw=|AF|+|BF| \           ,\ Obw=x+x \           ,\ Obw=2x$$ Otrzymaliśmy oczekiwaną wartość, zatem dowodzenie można uznać za zakończone.

Teoria:      
W trakcie opracowania