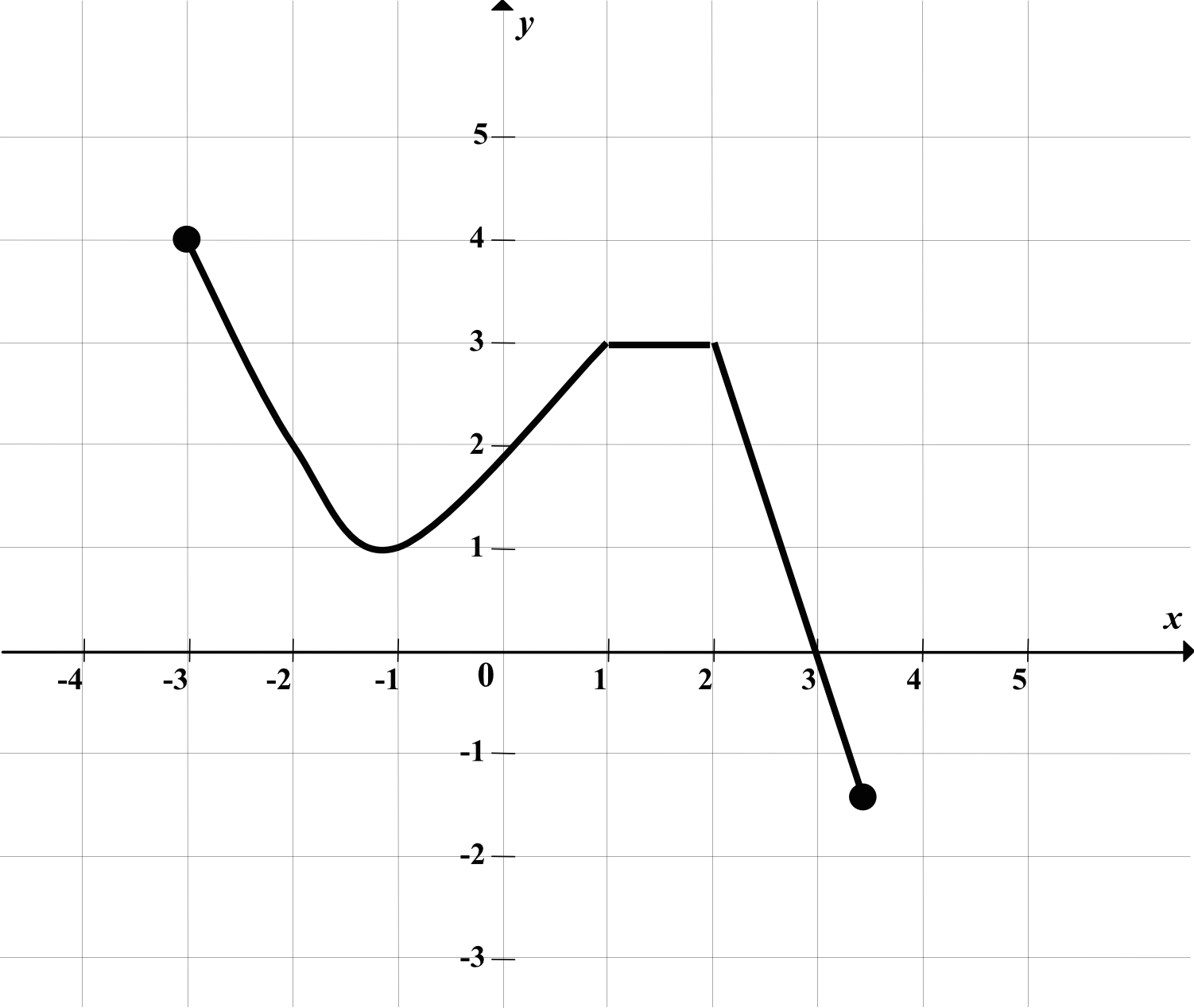Na rysunku przedstawiono wykres funkcji \(y=f(x)\).







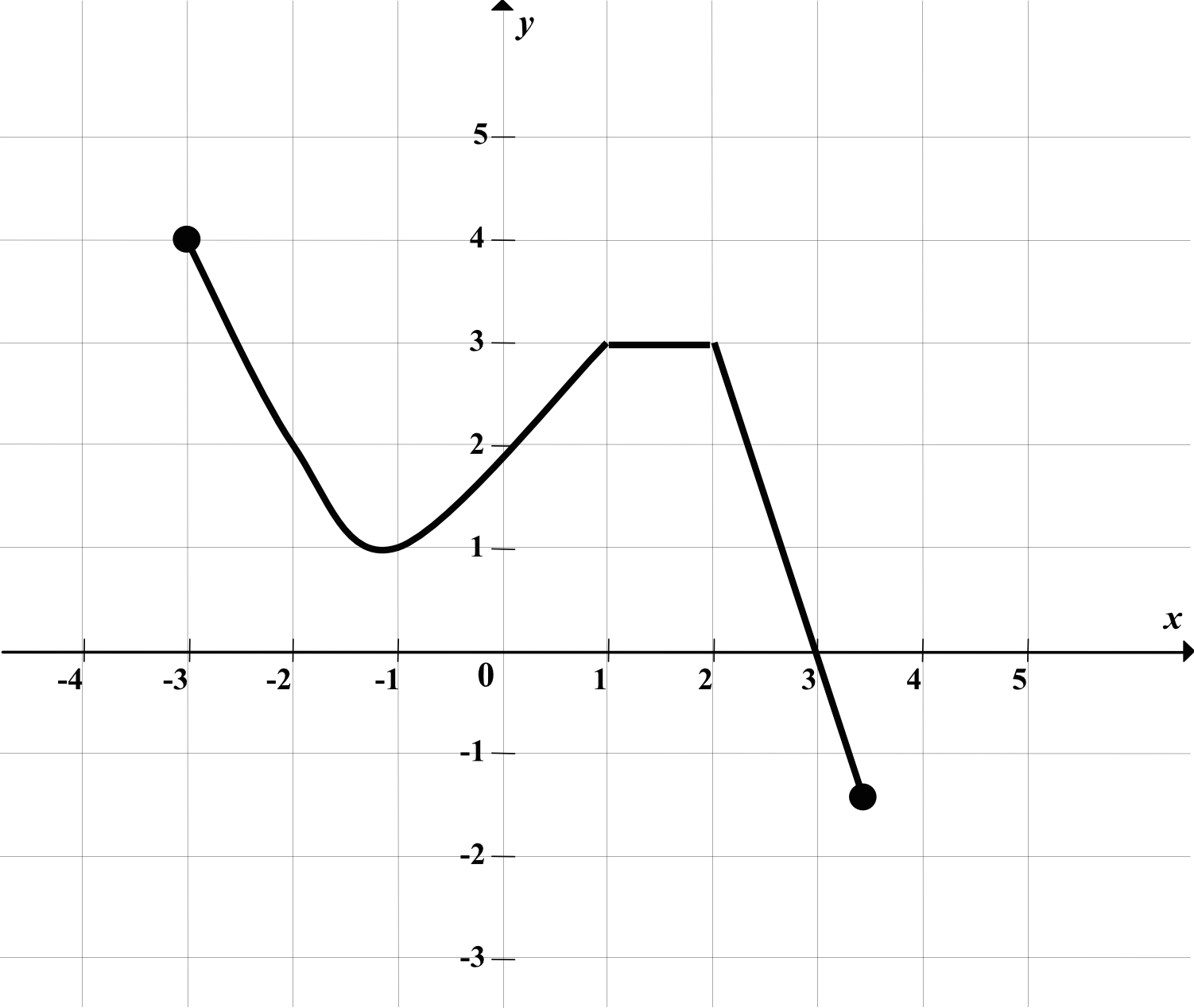
Największa wartość funkcji \(f\) w przedziale \(\langle-1,1\rangle\) jest równa:

A \(4\)
B \(3\)
C \(2\)
D \(1\)

Odpowiedź:      

B

Rozwiązanie:      
W tym zadaniu jest mała pułapka, bo musimy zwracać uwagę tylko i wyłącznie na przedział \(\langle-1,1\rangle\), a nie na cały wykres funkcji! Zbiór wartości i tym samym największą wartość funkcji odczytujemy z osi \(y\) (krótko mówiąc: będzie to najwyżej położony punkt). W naszym przypadku w przedziale \(\langle-1,1\rangle\) funkcja przyjmuje najwyższą wartość równą \(3\).

Teoria:      
W trakcie opracowania