Podstawą ostrosłupa prawidłowego trójkątnego \(ABCS\) jest trójkąt równoboczny \(ABC\). Pole ściany bocznej ostrosłupa jest dwa razy większe od pola jego podstawy. Wysokość \(SO\) tego ostrosłupa jest równa \(6\) (zobacz rysunek).





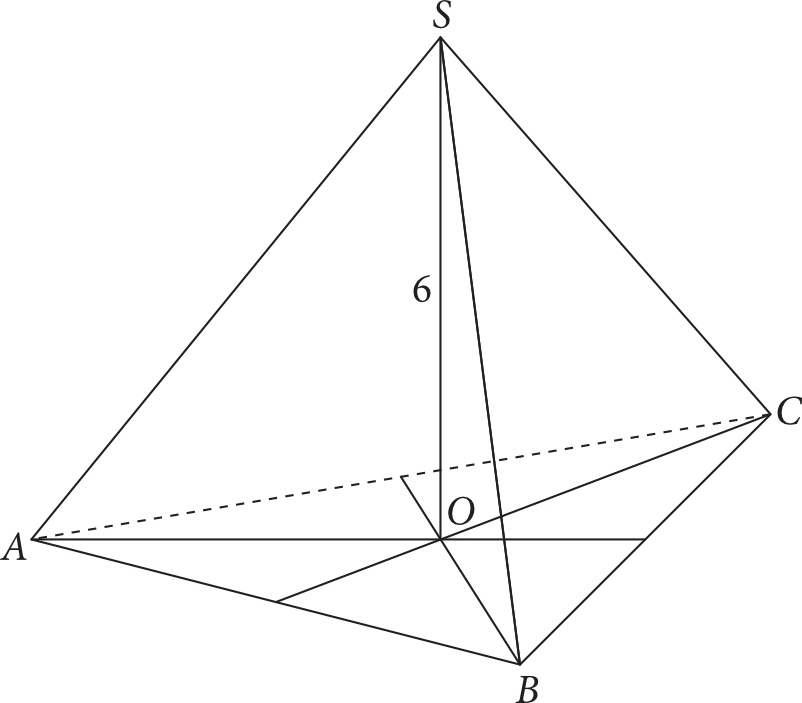
Wysokość ostrosłupa poprowadzona z wierzchołka \(C\) do ściany bocznej \(ABS\) jest równa:

A \(6\)
B \(4\)
C \(3\)
D \(2\)

Odpowiedź:      

C

Rozwiązanie:      
Krok 1. Sporządzenie rysunku pomocniczego. Zanim zaczniemy cokolwiek liczyć, spróbujmy zaznaczyć na rysunku jakiej wysokości szukamy, bo jest to dość rzadko spotykana sytuacja: Mówiąc bardziej obrazowo, szukamy wysokości ostrosłupa, tak jakby ostrosłup \(ABCS\) był przewrócony (trójkąt \(ABS\) byłby wtedy jego podstawą). Krok 2. Obliczenie wysokości ostrosłupa z wierzchołka \(C\). Niezależnie od tego jak jest ułożony ostrosłup, to jego objętość będzie taka sama i to będzie nasz punkt wyjścia do dalszych obliczeń. Jeżeli przyjmiemy, że pole podstawy \(ABC\) jest równe \(x\), to objętość ostrosłupa będzie równa: $$V=\frac{1}{3}\cdot P_{p}\cdot H \           ,\ V=\frac{1}{3}x\cdot6 \           ,\ V=2x$$ Z treści zadania wynika, że ściana boczna ma pole powierzchni dwa razy większe od podstawy. Tym samym pole ściany \(ABS\) będzie równe \(2x\). Jeżeli potraktujemy teraz ścianę \(ABS\) jako podstawę ostrosłupa, to opuszczona na nią wysokość z wierzchołka \(C\) musi być na tyle długa, by objętość bryły w dalszym ciągu była równa \(2x\), czyli: $$2x=\frac{1}{3}\cdot2x\cdot H_{C} \           ,\ H_{C}=3$$

Teoria:      
W trakcie opracowania