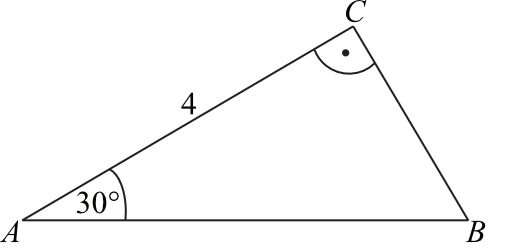
Pole trójkąta prostokątnego \(ABC\), przedstawionego na rysunku, jest równe:

A \(\frac{32\sqrt{3}}{6}\)
B \(\frac{16\sqrt{3}}{6}\)
C \(\frac{8\sqrt{3}}{3}\)
D \(\frac{4\sqrt{3}}{3}\)

Odpowiedź:      

C

Rozwiązanie:      
Krok 1. Obliczenie długości boku \(BC\). Długość boku \(BC\) możemy obliczyć korzystając z tangensa: $$tg30°=\frac{|BC|}{|AC|} \           ,\ \frac{\sqrt{3}}{3}=\frac{|BC|}{4} \quad\bigg/\cdot4 \           ,\ |BC|=\frac{4\sqrt{3}}{3}$$ Krok 2. Obliczenie pola powierzchni trójkąta. W trójkącie prostokątnym długości przyprostokątnych są jednocześnie długościami podstawy i wysokości trójkąta, zatem: $$P=\frac{1}{2}\cdot a\cdot h \           ,\ P=\frac{1}{2}\cdot4\cdot\frac{4\sqrt{3}}{3} \           ,\ P=2\cdot\frac{4\sqrt{3}}{3} \           ,\ P=\frac{8\sqrt{3}}{3}$$

Teoria:      
W trakcie opracowania