Na rysunku przedstawiono wykres funkcji \(f\) określonej w zbiorze \((-1,7)\).





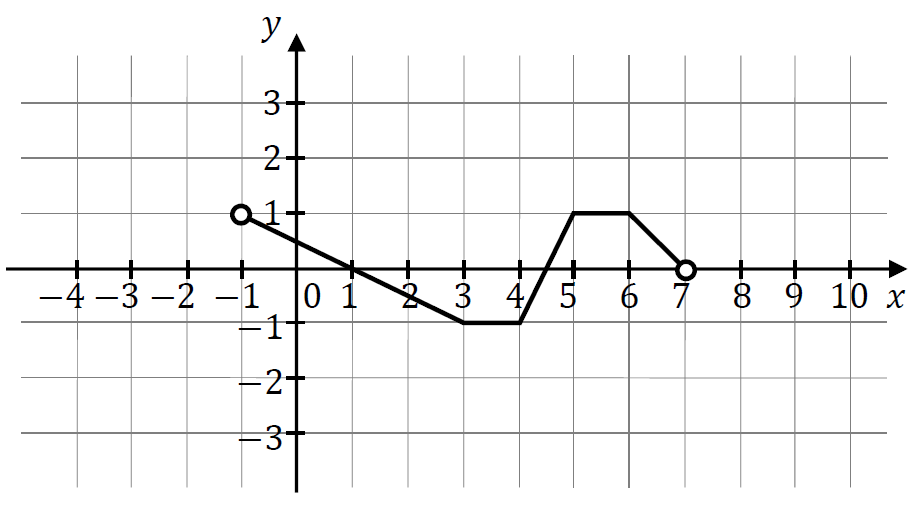
Wskaż zdanie prawdziwe.

A Funkcja \(f\) ma trzy miejsca zerowe
B Zbiorem wartości funkcji \(f\) jest \(\langle-1,1)\)
C Funkcja \(f\) osiąga wartość największą równą \(1\)
D Funkcja \(f\) osiąga wartości ujemne dla argumentów ze zbioru \((-1,0)\)

Odpowiedź:      

C

Rozwiązanie:      
Przeanalizujmy po kolei każdą z proponowanych odpowiedzi. Odp A. - to zdanie jest nieprawdą, gdyż nasza funkcja ma tylko dwa miejsca zerowe: \(x=1\) oraz \(x=4,5\). Gdyby ostatnia kropka była zamalowana, to wtedy miejscem zerowym byłoby jeszcze \(x=7\). Odp. B - to zdanie jest nieprawdą, gdyż nie zgadza się tutaj nawias przy liczbie \(1\). Owszem, po lewej stronie wykresu kropka jest niezamalowana, co mogłoby sugerować że wartość równa \(1\) nie jest przyjmowana, ale przecież wartość równa \(1\) jest przyjmowana chociażby dla argumentów \(x=5\) czy \(x=6\). Zbiorem wartości będzie więc tutaj \(\langle-1, 1\rangle\) Odp. C. - to zdanie jest prawdą, bowiem faktycznie największą wartością przyjmowaną przez tę funkcję jest \(1\) (ta wartość jest przyjmowana dla wszystkich argumentów od \(x=5\) aż do \(x=6\) włącznie). Odp. D. - to zdanie jest nieprawdą, gdyż ujemne wartości są przyjmowane dla argumentów ze zbioru \((1;4,5)\)

Teoria:      
W trakcie opracowania