Na rysunku przedstawiono fragment wykresu funkcji kwadratowej \(f\). Jednym z miejsc zerowych tej funkcji jest liczba \(2\). Do wykresu funkcji \(f\) należy punkt \((0,3)\). Prosta o równaniu \(x=-2\) jest osią symetrii paraboli, będącej wykresem funkcji \(f\).





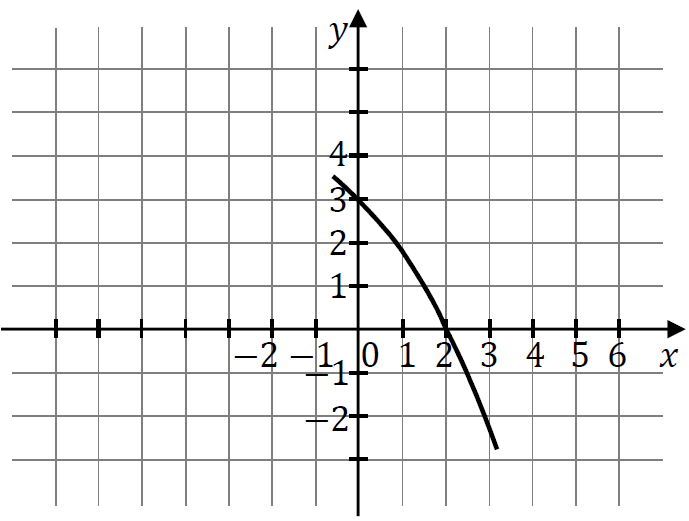
Drugim miejscem zerowym funkcji \(f\) jest liczba:

A \(-2\)
B \(-3\)
C \(-4\)
D \(-6\)

Odpowiedź:      

D

Rozwiązanie:      
Z własności funkcji kwadratowych wiemy, że miejsca zerowe są oddalone od osi symetrii o jednakową liczbę jednostek. Znane nam miejsce zerowe \(x=2\) jest oddalone od osi symetrii \(x=-2\) o \(4\) jednostki, wiec analogicznie poszukiwane miejsce zerowe także musi być o te \(4\) jednostki oddalone: Oczywiście do tego samego wyniku możemy dojść w nieco bardziej matematyczny sposób, przy użyciu średniej arytmetycznej. Wiedząc, że oś symetrii znajduje się dokładnie między dwoma miejscami zerowymi, moglibyśmy zapisać, że: $$\frac{x+2}{2}=-2 \           ,\ x+2=-4 \           ,\ x=-6$$

Teoria:      
W trakcie opracowania