Na okręgu o środku w punkcie \(O\) leżą punkty \(A\), \(B\) oraz \(C\). Odcinek \(AC\) jest średnicą tego okręgu, a kąt środkowy \(AOB\) ma miarę \(82°\) (zobacz rysunek).





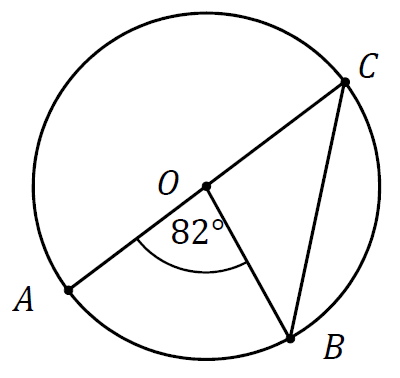
Miara kąta \(OBC\) jest równa:

A \(41°\)
B \(45°\)
C \(49°\)
D \(51°\)

Odpowiedź:      

A

Rozwiązanie:      
Krok 1. Obliczenie miary kąta \(BOC\). Wiemy, że suma kątów przyległych jest równa \(180°\), zatem: $$|\sphericalangle BOC|=180°-82°=98°$$ Krok 2. Obliczenie miary kąta \(OBC\). Spójrzmy na trójkąt \(BOC\). Jest to trójkąt równoramienny. Skąd to wiemy? Wynika to z tego, że ramiona \(BO\) oraz \(CO\) są jednocześnie promieniami okręgu. Wiemy już, że kąt między tymi ramionami ma miarę \(98°\), zatem suma miar dwóch pozostałych kątów musi być równa \(180°-98°=82°\). Z własności trójkątów równoramiennych wynika, że kąty przy podstawie muszą mieć jednakową miarę. Skoro tak, to: $$|\sphericalangle OBC|=82°:2=41°$$

Teoria:      
W trakcie opracowania