Odcinki \(AB\) i \(DE\) są równoległe. Długości odcinków \(CD\), \(DE\) i \(AB\) są odpowiednio równe \(1\), \(3\) i \(9\).







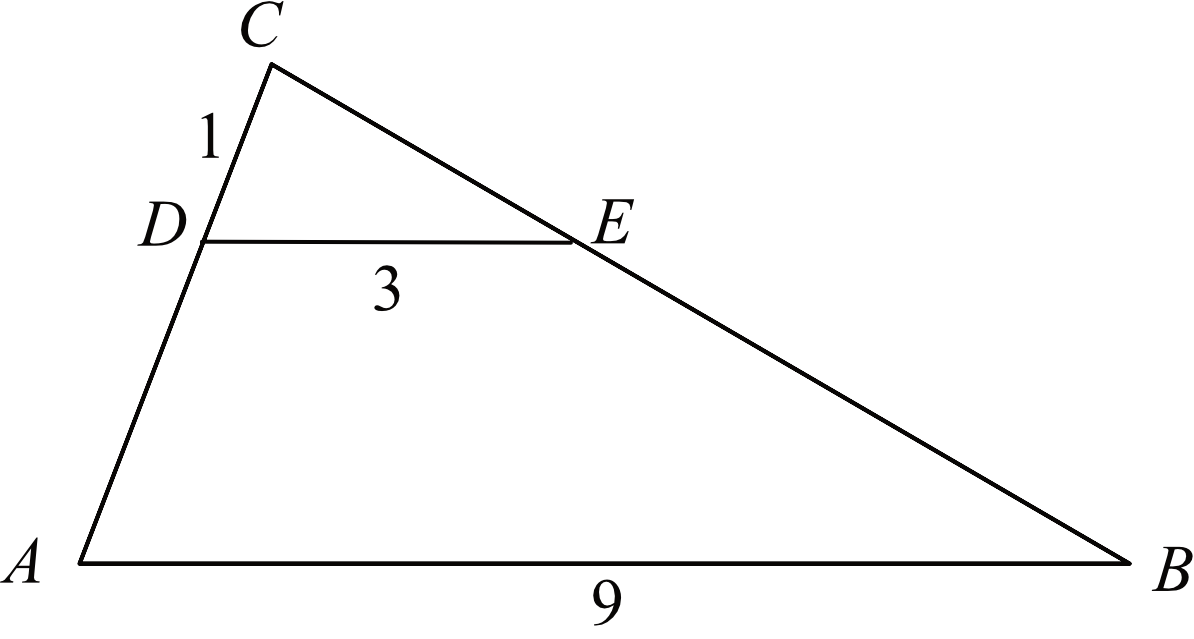
Długość odcinka \(AD\) jest równa:

A \(2\)
B \(3\)
C \(5\)
D \(6\)

Odpowiedź:      

A

Rozwiązanie:      
Skorzystamy tutaj z podobieństwa trójkątów \(CDE\) oraz \(CAB\). Krok 1. Ułożenie odpowiedniej proporcji długości boków i wyznaczenie długości odcinka \(CA\). $$\frac{|CD|}{|DE|}=\frac{|CA|}{|AB|} \           ,\ \frac{1}{3}=\frac{|CA|}{9}$$ Widzimy, że zgodnie z tą proporcją długość boku \(|CA|\) jest równa \(3\). Gdybyśmy tego nie dostrzegli, to można wykonać mnożenie na krzyż: $$1\cdot9=|CA|\cdot3 \           ,\ 3\cdot|CA|=9 \           ,\ |CA|=3$$ Krok 2. Obliczenie długości odcinka \(AD\). Korzystając z rysunku widzimy, że: $$|AD|=|CA|-1 \           ,\ |AD|=3-1 \           ,\ |AD|=2$$

Teoria:      
W trakcie opracowania