Odcinek \(BD\) jest zawarty w dwusiecznej kąta ostrego \(ABC\) trójkąta prostokątnego, w którym przyprostokątne \(AC\) i \(BC\) mają długości odpowiednio \(5\) i \(3\).





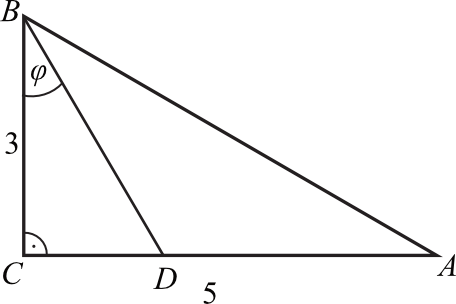
Wówczas miara \(φ\) kąta \(DBC\) spełnia warunek:

A \(20° \lt φ \lt 25°\)
B \(25° \lt φ \lt 30°\)
C \(30° \lt φ \lt 35°\)
D \(35° \lt φ \lt 40°\)

Odpowiedź:      

B

Rozwiązanie:      
Krok 1. Wprowadzenie poprawnych oznaczeń. Spójrzmy na kąt \(ABC\) i załóżmy że ma on miarę \(α\). O tym kącie wiemy, że jest dwukrotnie większy od poszukiwanego kąta \(φ\), czyli: $$|\sphericalangle ABC|=α=2φ$$ Krok 2. Obliczenie miary kąta \(ABC\). Znamy długości przyprostokątnej \(AC\) oraz \(BC\). Możemy więc posłużyć się funkcjami trygonometrycznymi i wyznaczyć miarę kąta \(ABC\), który umownie oznaczyliśmy jako \(α\). Korzystając z tangensa możemy zapisać, że: $$tgα=\frac{5}{3} \           ,\ tgα\approx1,67$$ Z tablic matematycznych musimy odczytać dla jakiego kąta tangens przyjmuje wartość bliską \(1,67\). Z takich tablic wynika, że dla kąta \(59°\) tangens przyjmuje wartość \(1,6643\) i jest to najlepsze przybliżenie jakie możemy otrzymać, zatem możemy zapisać, że: $$α\approx59°$$ Krok 3. Obliczenie miary kąta \(φ\). Wiemy, że kąt \(α\) jest dwukrotnie większy od kąta \(φ\), zatem: $$φ\approx59°:2\approx29,5°$$ W związku z tym prawidłową odpowiedzią jest nierówność \(25°\lt φ \lt30°\).

Teoria:      
W trakcie opracowania