W okręgu o środku \(O\) dany jest kąt wpisany \(ABC\) o mierze \(20°\) (patrz rysunek).





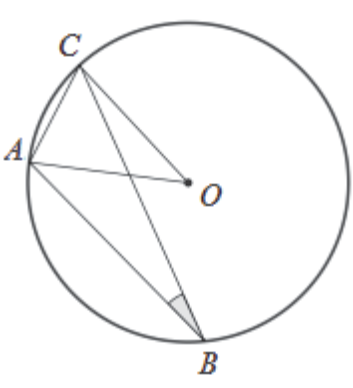
Miara kąta \(CAO\) jest równa:

A \(85°\)
B \(70°\)
C \(80°\)
D \(75°\)

Odpowiedź:      

B

Rozwiązanie:      
Krok 1. Obliczenie miary kąta \(AOC\). Kąt środkowy \(AOC\) jest oparty na tym samym łuku co kąt wpisany \(ABC\). Z własności kątów środkowych i wpisanych wiemy, że w takiej sytuacji kąt środkowy będzie mieć miarę dwukrotnie większą, zatem: $$|\sphericalangle AOC|=2\cdot20°=40°$$ Krok 2. Obliczenie miary kąta \(CAO\). Spójrzmy na trójkąt \(ACO\). Jest to trójkąt równoramienny, którego ramiona \(AO\) oraz \(CO\) mają długość równą promieniu okręgu. W trójkącie równoramiennym kąty przy podstawie mają jednakową miarę i to właśnie pozwoli nam wyznaczyć miarę kąta \(CAO\). Skoro \(|\sphericalangle AOC|=40°\), a suma kątów w trójkącie wynosi \(180°\), to znaczy że: $$|\sphericalangle CAO|=(180°-40°):2=140°:2=70°$$

Teoria:      
W trakcie opracowania