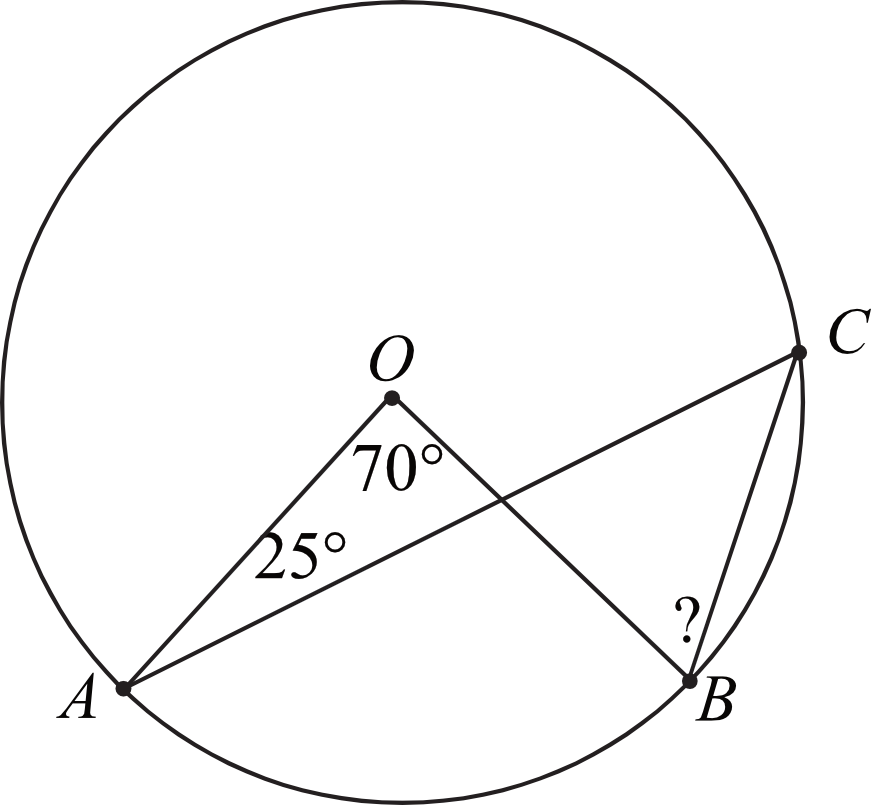
Na okręgu o środku w punkcie \(O\) wybrano trzy punkty \(A\), \(B\), \(C\) tak, że \(|\sphericalangle AOB|=70°\), \(|\sphericalangle OAC|=25°\). Cięciwa \(AC\) przecina promień \(OB\) (zobacz rysunek). Wtedy miara \(\sphericalangle OBC\) jest równa:

A \(α=25°\)
B \(α=60°\)
C \(α=70°\)
D \(α=85°\)

Odpowiedź:      

B

Rozwiązanie:      
Niech punkt przecięcia się cięciwy z odcinkiem AB to będzie punkt \(P\) (ułatwi nam to nazewnictwo kątów). Krok 1. Wyznaczenie miary kąta \(APO\). Spójrzmy na trójkąt \(OAP\). Znamy miary dwóch kątów tego trójkąta, zatem jesteśmy w stanie wyznaczyć miarę także trzeciego kąta: $$|\sphericalangle APO|=180°-25°-70°=85°$$ Krok 2. Wyznaczenie miary kąta \(BPC\). Kąt \(BPC\) jest kątem wierzchołkowym z kątem \(APO\), a z własności takich kątów wiemy, że mają jednakową miarę, zatem: $$|\sphericalangle BPC|=|\sphericalangle APO|=85°$$ Krok 3. Wyznaczenie miary kąta \(ACB\). Kąt \(ACB\) to kąt wpisany, który jest oparty na tym samym łuku co znany nam kąt środkowy o mierze \(70°\). Z własności kątów wpisanych i środkowych, które są oparte na tym samym łuku, wiemy że miara kąta wpisanego musi być dwukrotnie mniejsza od miary kąta środkowego, zatem: $$|\sphericalangle ACB|=70°:2=35°$$ Krok 4. Wyznaczenie miary kąta \(PBC\). Spójrzmy teraz na trójkąt \(PBC\). Znamy miary dwóch kątów w tym trójkącie, a jedyną niewiadomą jest poszukiwana przez nas miara kąta \(PBC\). Skoro suma kątów w trójkącie jest równa \(180°\), to: $$|\sphericalangle PBC|=180°-85°-35°=60°$$

Teoria:      
W trakcie opracowania