Podstawą ostrosłupa jest kwadrat \(ABCD\) o boku długości \(4\). Krawędź boczna \(DS\) jest prostopadła do podstawy i ma długość \(3\) (zobacz rysunek).





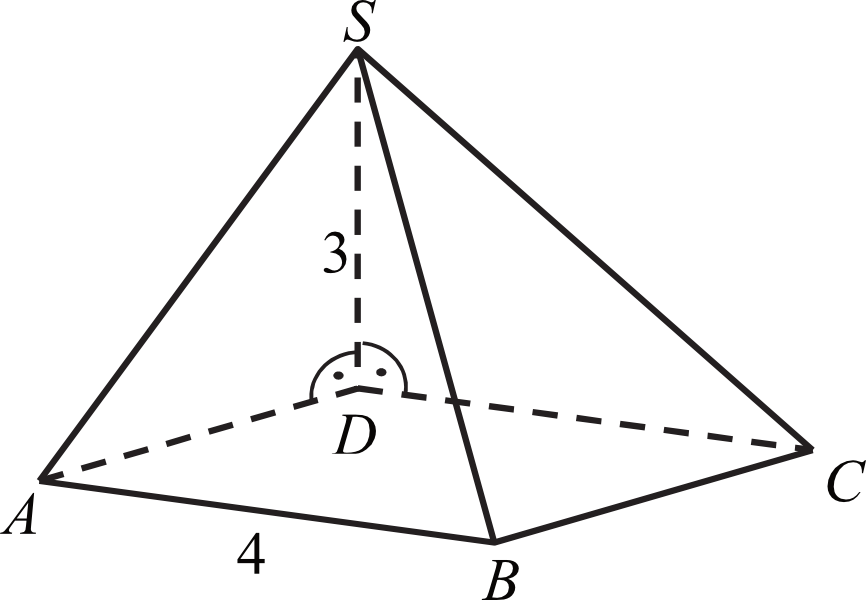
Pole ściany \(BCS\) tego ostrosłupa jest równe:

A \(20\)
B \(10\)
C \(16\)
D \(12\)

Odpowiedź:      

B

Rozwiązanie:      
Krok 1. Dostrzeżenie, że trójkąt \(BCS\) jest prostokątny. Kluczem do rozwiązania tego zadania jest dostrzeżenie tego, iż trójkąt \(BCS\) jest prostokątny (gdzie \(|\sphericalangle BCS|=90°\). Skąd to wiemy, skoro z rysunku takiej informacji nie możemy odczytać? Obliczmy długości poszczególnych boków tego trójkąta. Długość boku \(CS\): Spójrzmy na trójkąt prostokątny \(DCS\). Dolna przyprostokątna ma długość \(|DC|=4\), boczna przyprostokątna ma długość \(|DS|=3\), zatem z Twierdzenia Pitagorasa wynika, że: $$4^2+3^2=|CS|^2 \           ,\ 16+9=|CS|^2 \           ,\ |CS|^2=25 \           ,\ |CS|=5 \quad\lor\quad |CS|=-5$$ Ujemny wynik oczywiście odrzucamy, bo długość boku nie może być ujemna. W związku z tym \(|CS|=5\). Długość boku \(BS\): Spójrzmy na trójkąt \(BDS\). Dolna przyprostokątna to będzie przekątna naszego kwadratu znajdującego się w podstawie, czyli \(|BD|=4\sqrt{2}\). Boczna przyprostokątna ma długość \(|DS|=3\). W związku z tym: $$3^2+(4\sqrt{2})^2=|BS|^2 \           ,\ 9+16\cdot2=|BS|^2 \           ,\ 9+32=|BS|^2 \           ,\ |BS|^2=41 \           ,\ |BS|=\sqrt{41} \quad\lor\quad |BS|=-\sqrt{41}$$ Ujemny wynik odrzucamy, zatem zostaje nam \(|BS|=\sqrt{41}\). W tym momencie znamy długości trzech boków naszego trójkąta \(BCS\): $$|BC|=4 \           ,\ |CS|=5 \           ,\ |BS|=\sqrt{41}$$ Aby udowodnić, że jest to trójkąt prostokątny, skorzystamy z Twierdzenia Pitagorasa. Boki \(BC\) oraz \(CS\) to przyprostokątne, natomiast \(BS\) to przeciwprostokątna naszego trójkąta. W związku z tym: $$|BC|^2+|CS|^2=|BS|^2 \           ,\ 4^2+5^2=(\sqrt{41})^2 \           ,\ 16+25=41 \           ,\ 41=41 \           ,\ L=P$$ Skoro lewa strona równania jest równa prawej, to możemy być pewni, że trójkąt \(BCS\) jest trójkątem prostokątnym. Krok 2. Obliczenie pola powierzchni trójkąta \(BCS\). Skoro jest to trójkąt prostokątny i znamy miary przyprostokątnych tego trójkąta, to obliczenie pola powierzchni jest już tylko formalnością: $$P=\frac{1}{2}ah \           ,\ P=\frac{1}{2}\cdot4\cdot5 \           ,\ P=2\cdot5 \           ,\ P=10$$

Teoria:      
W trakcie opracowania