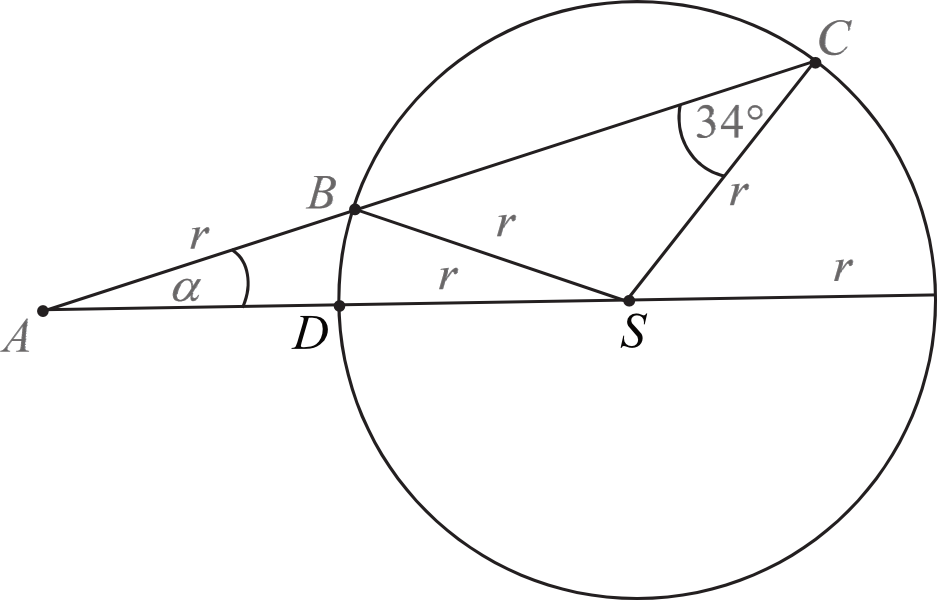
Punkty \(B\), \(C\) i \(D\) leżą na okręgu o środku \(S\) i promieniu \(r\). Punkt \(A\) jest punktem wspólnym prostych \(BC\) i \(SD\), a odcinki \(AB\) i \(SC\) są równej długości. Miara kąta \(BCS\) jest równa \(34°\) (zobacz rysunek).





Wtedy:

A \(α=12°\)
B \(α=17°\)
C \(α=22°\)
D \(α=34°\)

Odpowiedź:      

B

Rozwiązanie:      
Krok 1. Wyznaczenie miary kąta \(CBS\). Z rysunku wynika, że trójkąt \(BCS\) jest trójkątem równoramiennym (ramiona mają długość \(r\)), zatem kąty przy podstawie \(BC\) będą miały jednakową miarę. To oznacza, że: $$|\sphericalangle CBS|=|\sphericalangle BCS|=34°$$ Krok 2. Wyznaczenie miary kąta \(ABS\). Spójrzmy teraz na kąt \(ABS\), który jest kątem przyległym do obliczonego przed chwilą kąta \(CBS\). Suma kątów przyległych jest równa \(180°\), zatem: $$|\sphericalangle ABS|=180°-34°=146°$$ Krok 3. Wyznaczenie miary kąta \(α\). Teraz spójrzmy na trójkąt \(ASB\). To także trójkąt równoramienny (ramiona mają długość \(r\)), którego kąt między ramionami ma \(146°\). Skoro suma kątów w trójkącie jest równa \(180°\), to kąty przy podstawie \(AS\) mają łącznie: $$180°-146°=34°$$ Skoro jest to trójkąt równoramienny to kąty przy podstawie muszą mieć jednakową miarę, a to oznacza, że: $$α=34°:2=17°$$

Teoria:      
W trakcie opracowania