Trójkąt przedstawiony na rysunku jest ścianą boczną ostrosłupa prawidłowego trójkątnego.





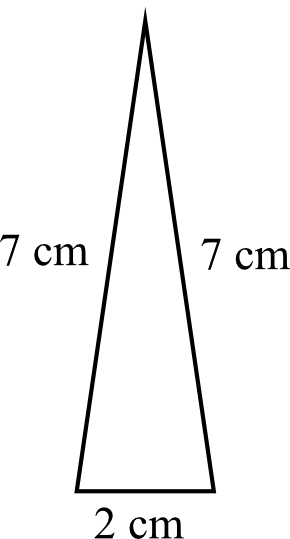
Oblicz pole powierzchni całkowitej tego ostrosłupa.

Odpowiedź:      

Pole powierzchni całkowitej tego ostrosłupa jest równe \(13\sqrt{3}cm^2\).

Rozwiązanie:      
Krok 1. Obliczenie pola podstawy. Wiemy, że ostrosłup jest ostrosłupem prawidłowym trójkątnym. To oznacza, że w podstawie musi znaleźć się trójkąt równoboczny. Z rysunku możemy od razu odczytać, że długość boku tego trójkąta znajdującego się w podstawie jest równa \(2cm\) (patrz rysunek), a skoro tak, to pole podstawy będzie równe: $$P_{p}=\frac{a^2\sqrt{3}}{4} \           ,\ P_{p}=\frac{2^2\sqrt{3}}{4} \\ P_{p}=\frac{4\sqrt{3}}{4} \           ,\ P_{p}=\sqrt{3}[cm^2]$$ Krok 2. Obliczenie wysokości ściany bocznej. Do obliczenia pola powierzchni całkowitej potrzebujemy znać jeszcze pola ściany bocznej. Aby ją obliczyć musimy poznać wysokość trójkąta i tu skorzystamy z Twierdzenia Pitagorasa oraz z własności trójkątów równoramiennych, która mówi nam że wysokość takiego trójkąta dzieli podstawę na dwie równe części. Z Twierdzenia Pitagorasa otrzymamy: $$1^2+h^2=7^2 \           ,\ 1+h^2=49 \           ,\ h^2=48 \           ,\ h=\sqrt{48}=\sqrt{16\cdot3}=4\sqrt{3}[cm]$$ Krok 3. Obliczenie pola powierzchni pojedynczej ściany bocznej. Wiemy już, że w ścianie bocznej znajduje się trójkąt o podstawie \(2cm\) oraz wysokości \(4\sqrt{3}cm\), zatem jego pole powierzchni będzie równe: $$P_{b}=\frac{1}{2}\cdot2\cdot4\sqrt{3} \           ,\ P_{b}=1\cdot4\sqrt{3} \           ,\ P_{b}=4\sqrt{3}[cm^2]$$ Krok 4. Obliczenie pola powierzchni całkowitej. Na pole powierzchni całkowitej składają się jedna podstawa oraz trzy ściany boczne, zatem: $$P_{c}=P_{p}+3P_{b} \           ,\ P_{c}=\sqrt{3}+3\cdot4\sqrt{3} \           ,\ P_{c}=\sqrt{3}+12\sqrt{3} \           ,\ P_{c}=13\sqrt{3}[cm^2]$$

Teoria:      
W trakcie opracowania