Dany jest romb \(ABCD\). Obwód tego rombu jest równy \(52 cm\), a przekątna \(AC\) ma długość \(24 cm\) (zobacz rysunek poniżej).





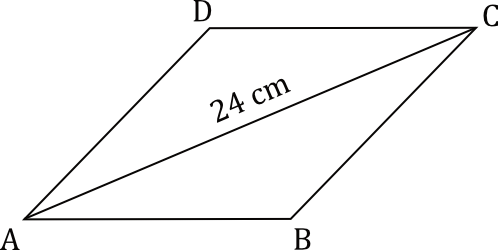
Oblicz długość przekątnej \(BD\) rombu \(ABCD\). Zapisz obliczenia.

Odpowiedź:      

\(10cm\)

Rozwiązanie:      
Krok 1. Obliczenie długości boku rombu. Skoro obwód rombu jest równy \(52cm\), a każdy bok rombu ma jednakową długość, to: $$a=52cm:4 \           ,\ a=13cm$$ Krok 2. Sporządzenie rysunku pomocniczego. Przekątne rombu przecinają się w połowie swojej długości. To oznacza, że sytuacja z treści zadania będzie wyglądać następująco: Powstał nam trójkąt prostokątny, z którego teraz musimy wyznaczyć długość połowy przekątnej \(BD\). Krok 3. Obliczenie długości połowy przekątnej \(BD\) (czyli \(x\)). Korzystając z zaznaczonego trójkąta prostokątnego obliczmy najpierw długość boku \(x\), który jest połową przekątnej \(BD\). Z twierdzenia Pitagorasa wynika, że: $$12^2+x^2=13^2 \           ,\ 144+x^2=169 \           ,\ x^2=25 \           ,\ x=5 \quad\lor\quad x=-5$$ Ujemny wynik oczywiście odrzucamy, bo długość boku musi być dodatnia. Zostaje nam więc \(x=5\). Krok 4. Obliczenie długości przekątnej \(BD\). Przekątna \(BD\) będzie dwa razy dłuższa od wyznaczonego odcinka \(x\), zatem: $$|BD|=2\cdot5 \           ,\ |BD|=10$$

Teoria:      
W trakcie opracowania