Dany jest trójkąt \(ABC\), w którym kąt \(BCA\) ma miarę \(35°\). Punkt \(D\) leży na boku \(BC\) tego trójkąta. Odcinek \(AD\) ma taką samą długość jak odcinek \(BD\). Kąt \(ADC\) ma miarę \(130°\) (zobacz rysunek poniżej).





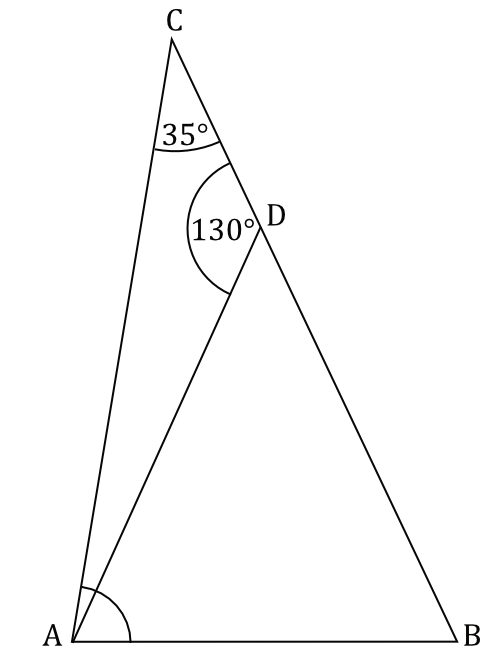
Kąt \(CAB\) ma miarę:

A \(95°\)
B \(75°\)
C \(90°\)
D \(80°\)

Odpowiedź:      

D

Rozwiązanie:      
Krok 1. Obliczenie miary kąta \(CAD\). Spójrzmy na trójkąt \(ADC\). Znamy dwie miary kątów w tym trójkącie, a skoro suma miar kątów w trójkątach jest równa \(180°\), to: $$|\sphericalangle CAD|=180°-130°-35°=15°$$ Krok 2. Obliczenie miary kąta \(ADC\). Kąt \(ADB\) jest kątem przyległym do kąta \(ADC\), a skoro suma miar kątów przyległych wynosi \(180°\), to: $$|\sphericalangle ADC|=180°-130°=50°$$ Krok 3. Obliczenie miary kąta \(DAB\). Spójrzmy na trójkąt \(ABD\). Z treści zadania wynika, że jest to trójkąt równoramienny i wiemy już, że kąt między ramionami ma miarę \(50°\). Skoro tak, to na dwa kąty przy podstawie zostaje nam \(180°-50°=130°\). W trójkątach równoramiennych kąty przy podstawie mają jednakową miarę, a to oznacza, że: $$|\sphericalangle DAB|=130°:2=65°$$ Krok 4. Obliczenie miary kąta \(CAB\). Kąt \(CAB\) jest sumą kątów \(CAD\) oraz \(DAB\), zatem: $$|\sphericalangle CAB|=15°+65°=80°$$

Teoria:      
W trakcie opracowania