Na rysunku przedstawiono trapez \(KLMN\) zbudowany z trzech jednakowych trójkątów prostokątnych o przyprostokątnych długości \(3 cm\) i \(4 cm\).





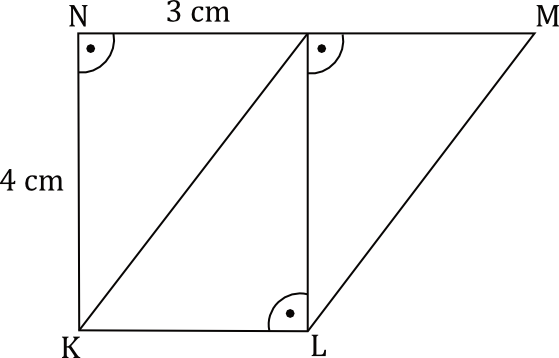
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe. Pole trapezu \(KLMN\) jest równe \(18 cm^2\)
Obwód trapezu \(KLMN\) jest równy \(18 cm\)

Pole trapezu \(KLMN\) jest równe \(18 cm^2\)

Odpowiedź:      

1) PRAWDA

2) PRAWDA

Rozwiązanie:      
Krok 1. Obliczenie długości boku \(LM\). Z treści zadania wynika, że wszystkie trójkąty są jednakowe. Z rysunku widzimy, że każdy trójkąt ma długości przyprostokątnych równe \(3cm\) oraz \(4cm\). Skoro tak, to długość przeciwprostokątnej takiego trójkąta (czyli tym samym długość boku \(LM\)) wyniesie: $$3^2+4^2=c^2 \           ,\ 9+16=c^2 \           ,\ c^2=25 \           ,\ c=5 \quad\lor\quad c=-5$$ Ujemną długość oczywiście odrzucamy, zatem zostaje nam \(c=5\), czyli \(|LM|=5\). Krok 2. Ocena prawdziwości pierwszego zdania. Pole trapezu będzie równe: $$P=\frac{1}{2}\cdot(a+b)\cdot h \           ,\ P=\frac{1}{2}\cdot(3cm+6cm)\cdot4cm \           ,\ P=\frac{1}{2}\cdot9cm\cdot4cm \           ,\ P=18cm^2$$ Pierwsze zdanie jest więc prawdą. Krok 3. Ocena prawdziwości drugiego zdania. Obwód naszego trapezu będzie równy: $$3cm+5cm+3cm+3cm+4cm=18cm$$ Zdanie jest więc prawdą.

Teoria:      
W trakcie opracowania