Na rysunku przedstawiono czworokąt \(ABCD\), w którym poprowadzono przekątną \(BD\).





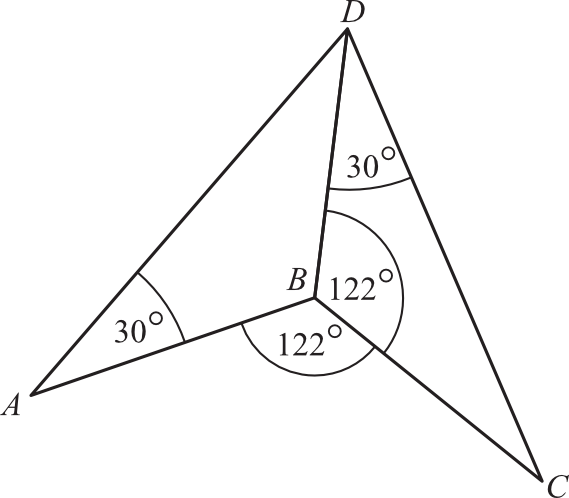
Czy przekątna \(BD\) podzieliła czworokąt na dwa trójkąty przystające? Wybierz odpowiedź T lub N i jej uzasadnienie spośród A, B lub C. A) suma kątów wewnętrznych w obu trójkątach jest taka sama.
B) przekątna \(BD\) jest wspólnym bokiem obu trójkątów i każdy z nich ma kąt \(30°\).
C) kąty wewnętrzne przy wierzchołku \(B\) w obu trójkątach są różnej miary.

Odpowiedź:      

Nie ponieważ opcja C

Rozwiązanie:      
Dwa trójkąty są przystające wtedy, gdy mają one jednakowe miary boków i jednakowe miary kątów. Miar boków nie jesteśmy w stanie zweryfikować, możemy jedynie przyjrzeć się miarom kątów. Spróbujmy wyznaczyć miarę kąta \(ABD\). Miara tego kąta będzie równa: $$|\sphericalangle ABD|=360°-122°-122°=116°$$ Widzimy zatem, że kąty w trójkącie \(ABD\) mają inną miarę nić w trójkącie \(BCD\), co sprawia, iż te trójkąty na pewno nie są przystające. Prawidłową odpowiedzią będzie zatem "Nie, ponieważ kąty wewnętrzne przy wierzchołku \(B\) w obu trójkątach są różnej miary".

Teoria:      
W trakcie opracowania