Na poniższej tablicy podano kolejne liczby naturalne w pięciu ponumerowanych rzędach.





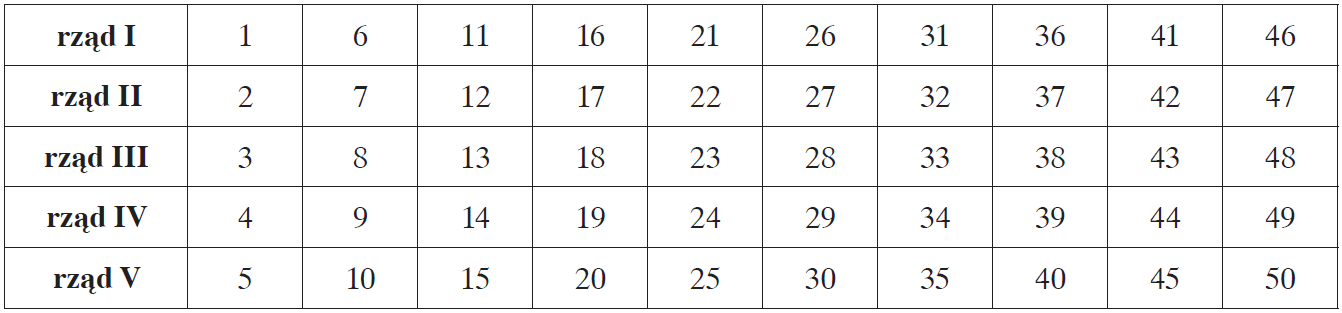
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zadanie jest prawdziwe, lub F, jeśli jest fałszywe. Prawdopodobieństwo wylosowania parzystej liczby z rzędu oznaczonego liczbą pierwszą jest mniejsze niż \(\frac{1}{2}\).
Prawdopodobieństwo, że losowo wybrana liczba z tablicy zawiera w zapisie cyfrę \(4\) wynosi \(0,3\).

Prawdopodobieństwo wylosowania parzystej liczby z rzędu oznaczonego liczbą pierwszą jest mniejsze niż \(\frac{1}{2}\).

Odpowiedź:      

1) FAŁSZ

2) FAŁSZ

Rozwiązanie:      
Krok 1. Ocena prawdziwości pierwszego zdania. Liczbami pierwszymi są \(2\), \(3\) oraz \(5\), więc interesują nas jedynie rzędy II, III oraz V. W każdym z tych rzędów mamy \(10\) miejsc, czyli w tych trzech analizowanych rzędach mamy łącznie \(3\cdot10=30\) miejsc. W każdym interesującym nas rzędzie mamy \(5\) miejsc oznaczonych liczbą parzystą, czyli interesujących nas miejsc jest łącznie \(3\cdot5=15\). Skoro tak, to prawdopodobieństwo wylosowania liczby parzystej w każdym z tych rzędów będzie równe: $$p=\frac{15}{30}=\frac{1}{2}$$ Zdanie jest więc fałszem. Krok 2. Ocena prawdziwości drugiego zdania. Liczbami zawierającymi czwórkę są: $$4, 14, 24, 34, 40, 41, 42, \           ,\ 43, 44, 45, 46, 47, 48, 49$$ Łącznie mamy więc \(14\) takich liczb. Skoro wszystkich liczb jest \(50\), to prawdopodobieństwo wylosowania nas interesującej liczby z czwórką będzie równe: $$p=\frac{14}{50}=\frac{28}{100}=0,28$$ Zdanie jest więc fałszem.

Teoria:      
W trakcie opracowania