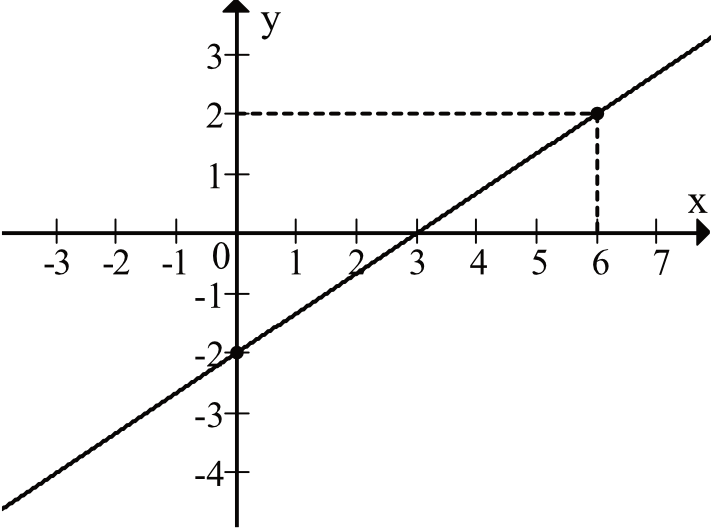Na rysunku przedstawiony jest fragment prostej o równaniu y=ax+b przechodzącej przez punkty \((0,-2)\) i \((6,2)\).







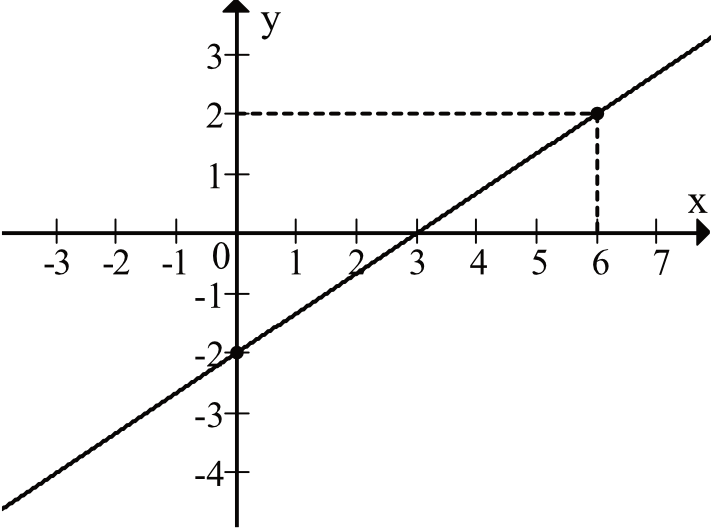
Wtedy:

A \(a=\frac{2}{3}, b=-2\)
B \(a=3, b=-2\)
C \(a=\frac{3}{2}, b=2\)
D \(a=-3, b=2\)

Odpowiedź:      

A

Rozwiązanie:      
Krok 1. Wyznaczenie wartości współczynnika \(b\). Współczynnik \(b\) mówi nam o tym gdzie dana prosta przecina się z osią \(Oy\). Skoro nasza prosta przechodzi przez punkt \((0;-2)\) to już wiemy, że \(b=-2\). Krok 2. Wyznaczenie wartości współczynnika \(a\). Po uzyskaniu informacji, że \(b=-2\) wiemy, że wzór naszej funkcji przyjmuje postać \(y=ax-2\). Podstawiając pod ten wzór współrzędne punktu \((6;2)\) wyznaczymy wartość współczynnika \(a\), zatem: $$y=ax-2 \           ,\ 2=6a-2 \           ,\ 6a=4 \           ,\ a=\frac{4}{6}=\frac{2}{3}$$

Teoria:      
W trakcie opracowania