Na rysunku przedstawiono interpretację geometryczną jednego z niżej zapisanych układów równań:





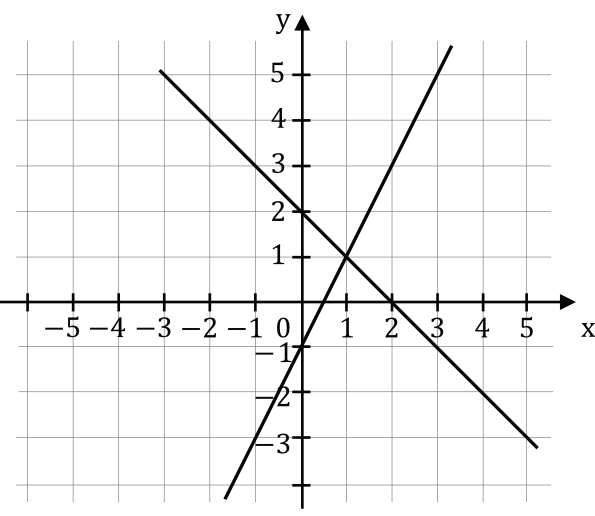
Wskaż ten układ równań, którego interpretację geometryczną przedstawiono na rysunku.

A \(\begin{cases}
y=-x+2 \           ,\
y=-2x+1
\end{cases}\)
B \(\begin{cases}
y=x-2 \           ,\
y=-2x-1
\end{cases}\)
C \(\begin{cases}
y=x-2 \           ,\
y=2x+1
\end{cases}\)
D \(\begin{cases}
y=-x+2 \           ,\
y=2x-1
\end{cases}\)

Odpowiedź:      

D

Rozwiązanie:      
Oczywiście moglibyśmy po prostu wyznaczyć równania tych dwóch prostych (wystarczy odczytać z rysunku współrzędne dwóch punktów przez które taka prosta przechodzi i skorzystać albo ze wzoru z tablic albo z tak zwanej metody układu równań). Nie mniej jednak w tego typu zadaniach bardzo często jesteśmy w stanie podać prawidłową odpowiedzieć jedynie analizując całą sytuację na rysunku. Po pierwsze powinniśmy dostrzec, że jedna prosta jest rosnąca, a druga malejąca. To oznacza, że jedna prosta powinna mieć dodatni współczynnik \(a\), natomiast druga powinna mieć ujemny. Taką sytuację mamy jedynie w odpowiedziach B oraz D, więc tylko do tych odpowiedzi możemy się ograniczyć. Po drugie - moglibyśmy dostrzec, że prosta malejąca przecina oś \(OY\) dla \(y=2\), co z kolei mówi nam, że ta prosta ma współczynnik \(b=2\). Taka sytuacja jest właśnie w odpowiedzi D, zatem bez żadnego liczenia możemy być pewni, że prawidłowym układem równań będzie ten z ostatniej odpowiedzi.

Teoria:      
W trakcie opracowania