Zbiory arkuszy maturalnych z matematyki. Nasza strona oferuje bogaty wybór przykładowych arkuszy, rozwiązań zadań, testów z matematyki oraz wiele innych materiałów
Informator maturalny CKE 2023 Zadanie 39 z 50
Zadanie nr 39. (1pkt)
Proste \(k\) i \(l\) przecinają się w punkcie \(A\). Proste \(m\), \(n\) i \(s\) są do siebie równoległe i przecinają obie proste \(k\) i \(l\) w punktach \(B, C, D, E, F, G\) (zobacz rysunek poniżej), w taki sposób, że:
$$|BC|=30, |CD|=20, |GF|=21$$
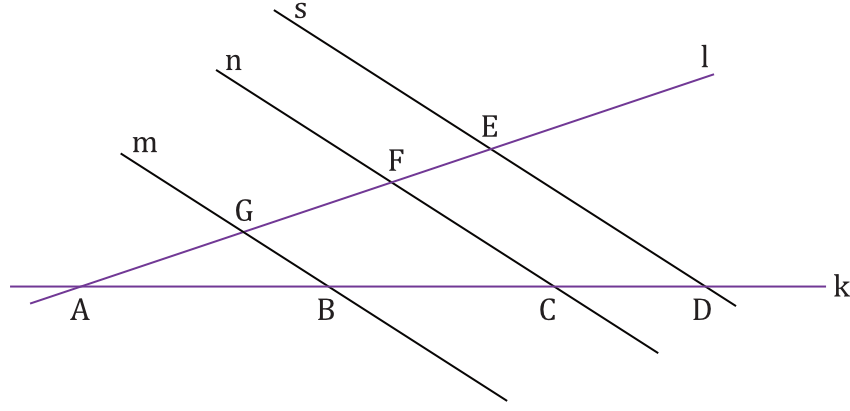
Oblicz długość odcinka \(FE\).
Rozwiązanie:
Korzystając z Twierdzenia Talesa możemy zapisać, że:
$$\frac{|GF|}{|BC|}=\frac{|FE|}{|CD|}$$
Podstawiając dane z treści zadania, otrzymamy:
$$\frac{21}{30}=\frac{|FE|}{20} \ ,\
|FE|=14$$
Teoria:
W trakcie opracowania
materiał edukacyjny - CKE

