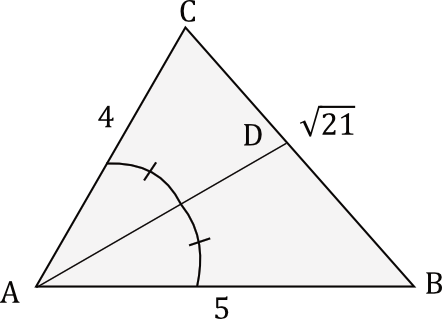
Dany jest trójkąt \(ABC\), w którym \(|AB|=5\), \(|BC|=\sqrt{21}\), \(|AC|=4\). Dwusieczna kąta \(\sphericalangle CAB\) przecina bok \(BC\) w punkcie \(D\) (zobacz rysunek poniżej).





Dokończ zdanie. Zaznacz odpowiedź \(A\), \(B\) albo \(C\) oraz jej uzasadnienie 1., 2. albo 3.



Długość odcinka \(BD\) jest równa:



A. \(|BD|=\frac{1}{2}\sqrt{21}\)

B. \(|BD|=\frac{5}{9}\sqrt{21}\)

C. \(|BD|=\frac{4}{5}\sqrt{21}\)



ponieważ z twierdzenia o dwusiecznej wynika, że:



1. \(\frac{|AB|}{|AC|}=\frac{|BC|}{|BD|}\)

2. \(|BD|=|DC|\)

3. \(\frac{|AB|}{|AC|}=\frac{|BD|}{|DC|}\)

Odpowiedź:      

B, ponieważ 3.

Rozwiązanie:      
Z twierdzenia o dwusiecznej kąta, wynika, że stosunek długości jednego ramienia (czyli \(AB\)) względem drugiego ramienia (czyli \(AC\)), musi być taki sam jak stosunek długości odcinka \(BD\) względem \(DC\). Matematycznie zapis będzie wyglądał następująco: $$\frac{|AB|}{|AC|}=\frac{|BD|}{|DC|}$$ Podstawiając do tego równania dane z rysunku, otrzymamy: $$\frac{5}{4}=\frac{|BD|}{|DC|} \           ,\ |BD|=\frac{5}{4}|DC|$$ Odcinek \(|DC|\) ma miarę \(\sqrt{21}-|BD|\), zatem: $$|BD|=\frac{5}{4}\cdot(\sqrt{21}-|BD|) \           ,\ |BD|=\frac{5}{4}\cdot\sqrt{21}-\frac{5}{4}|BD| \           ,\ \frac{9}{4}|BD|=\frac{5}{4}\cdot\sqrt{21} \quad\bigg/\cdot\frac{4}{9} \           ,\ |BD|=\frac{5}{9}\sqrt{21}$$

Teoria:      
W trakcie opracowania